Database Programming

The code in Example 2.4 is a case of the so called database programming: it acts as a database, where facts store the basic relationships among data (in much the same way as in relational databases), and the rules express new relationships among data, based on the ones we already have: in other words, they provide views to the database, but everything is seen, together, as a program which can answer to queries.

This language, although limited (for example, no data structures are used), can model quite sophisticated relationships, and answer queries which are not trivial.

Example 2.11   A logical circuit. Figure 2.3 depicts an electronic circuit implementing logic gates. Some parts of it (resistors and transistors) are labeled. We will use facts to construct a small database stating which components connect the different points highlighted in the circuit:

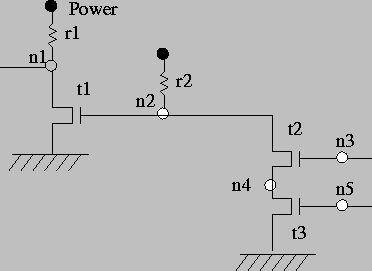
resistor(power,n1).
resistor(power,n2).
transistor(n2,ground,n1).
transistor(n3,n4,n2).
transistor(n5,ground,n4).

Note that current direction is meaningless in resistors, but for simplicity we have chosen to use the first argument of the facts defining resistors to denote the end connected to the power.

Some knowledge of electronic gates tells us that an inverter can be built of a transistor appropriately connected to a resistor. The needed connections are reflected in this rule:

inverter(Input,Output):-
   transistor(Input,ground,Output),
   resistor(power,Output).

Similar rules can be written for nand and and gates:

nand_gate(Input1,Input2,Output):-
   transistor(Input1,X,Output),
   transistor(Input2,ground,X),
   resistor(power,Output).
and_gate(Input1,Input2,Output):-
   nand_gate(Input1,Input2,X),
   inverter(X, Output).

The following query and answer demonstrate the knowledge of the problem about our circuit:

?- and_gate(In1,In2,Out).
   In1=n3, In2=n5, Out=n1}

Similarly, queries could be made to find out the connection points of inverters and and gates. $\blacksquare$

Problem 2.6   In Example 2.11, how could the code be modified so that it does not matter whether the resistors are defined as having power in the first or in the second argument? In other words, change and/or augment the rules for the circuit components so that whoever defines resistor/2 does not have to know about the differences between the first and the second argument. $\blacklozenge$

  

Figure 2.3: An electronic circuit