Subsections

• Problem:
• Solution:

The Blocks World

Problem:

  

Figure 7.1: A scenario in the blocks world

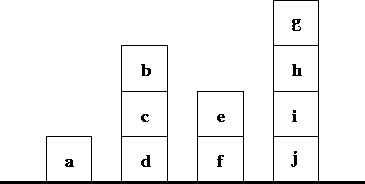
For this project we will only need a language having the = / 2 constraint, meaning syntactic equality. Consider a world with blocks having the setup shown in Figure 7.1. We will identify blocks with the names appearing in the picture. The following predicates will model the world:

on_floor(B):

B is leaning on the floor.

on(B1, B2):

block B1 is put directly on block B2.

at_left(B1, B2):

blocks B1 and B2 are put on the floor, and block B1 is directly at the left of B2.

The task to do is:

1.

Write a database of facts which models the world in the picture.

2.

Based exclusively on these facts, write the following predicates:

base(B1, B2):

B2 is the base of the pile containing B1.

base_at_right(B1, B2):

B1 and B2 are on the floor, and b2 is at the right (but perhaps not directly) of B1.

object_at_right(B1, B2):

B1 is in a pile which is at the right (but perhaps not directly) of B1.

The above predicates must work for any world defined using the facts on_floor/1, on/2, and at_left/2.

3.

There are several types of blocks, which can be piled or not on each other, depending on their physical shape. The following types of objects can appear: cubes, spheres, pyramids and toruses. We want to know if a configuration is physically stable using certain rules. A torus can be piled on any object, and, in fact, it is the only object which can be piled on a pyramid; in that case, the top of the pyramid will stick out from the torus, and the only object which can be piled on that torus is another torus. Any object can then be piled on that second torus. In particular, a torus is the only object on which a sphere can be piled (floor included).

Write a predicate which relates every object with its type, as shown below:

Object	Type
a	pyramid
b	torus
c	cube
d	sphere
e	cube
f	torus
g	torus
h	sphere
i	torus
j	pyramid

Using the type of each object and the predicates related to the position of objects in the world, write the following predicate:

unstable(O):

the object O is placed unstably on its base in the configuration known by the program.

Solution:

The predicates which model the basic relationships of the world are easy to work out:

on_floor(a).
on_floor(d).
on_floor(f).
on_floor(j).

on(c, d).
on(b, c).
on(e, f).
on(i, j).
on(h, i).
on(g, h).

at_left(a, d).
at_left(d, f).
at_left(f, j).

The predicate base/2 traverses down the pile until the block directly on the floor is found:

base(X, X):-
   on_floor(X).
base(X, Y):-
   on(X, Z),
   base(Z, Y).

base_at_right/2 follows the same idea as base/2, but it traverses the floor in search of contiguous blocks. We use the at_left/2 predicate (which ensures that both blocks are on the floor) and the recursion stops when both blocks are directly one at the left of the other.

base_at_right(X, Y):-
   at_left(X, Y).
base_at_right(X, Y):-
   at_left(X, Z),
   base_at_right(Z, Y).

Identifying X and Y such that the pile of X is to the right of that of Y is done by finding which object is at the bottom of each pile, and then ensuring that the first base (Xb) is at the right of the second one (Yb).

object_at_right(X, Y):-
   base(X, Xb),
   base(Y, Yb),
   base_at_right(Xb, Yb).

Relating the object with its type boils down to applying the techniques discussed in Section 2.6. Using a set of predicates of the form pyramid(a)., torus(b)., and so on, could have been possible, but in that case querying for the type of a block would not have been easy.

type_of(a, pyramid).
type_of(b, torus).
type_of(c, cube).
type_of(d, sphere).
type_of(e, cube).
type_of(f, torus).
type_of(g, torus).
type_of(h, sphere).
type_of(i, torus).
type_of(j, pyramid).

The predicate for instability is the less straightforward one, due to the number of possible cases. We will divide the unstable objects in three cases, which summarize the possible non-stable configurations:

1.

A sphere standing directly on the floor.

2.

A sphere standing on a cube.

3.

An object which is not a torus, and which is standing on a configuration which is convex; we define a configuration as being convex if there is no flat surface at its top on which a non-torus can stand still (i.e., pyramids, spheres, and pyramids which have only one torus on top of them).

no_torus(O):- type_of(O, pyramid).
no_torus(O):- type_of(O, cube).
no_torus(O):- type_of(O, sphere).

convex(O):- type_of(O, pyramid).
convex(O):- type_of(O, sphere).
convex(O):-
   type_of(O, torus),
   on(O, O1),
   type_of(O1, pyramid).

unstable(O):-
   type_of(O, sphere),
   on_floor(O).
unstable(O):-
   type_of(O, sphere),
   on(O, O1),
   type_of(O1, cube).
unstable(O):-
   no_torus(O),
   on(O, O1),
   convex(O1).