|
The cut is one of the Prolog operators related to the program control flow. It can be placed anywhere a goal can, and it is written as the predicate !/0. Technically, the cut commits the execution to all the choices made since the parent goal was unified with the head of the clause in which the cut appears. This means that all clauses below the one with the cut are discarded, as if they did not exist for this particular call (so they are not considered if the execution of the current clause fails, in which case the call to the predicate fails), and all the alternatives left by the execution of the goals at the left of the cut in that clause are also discarded. The goals at the right of the cut are executed normally (i.e., they can backtrack).
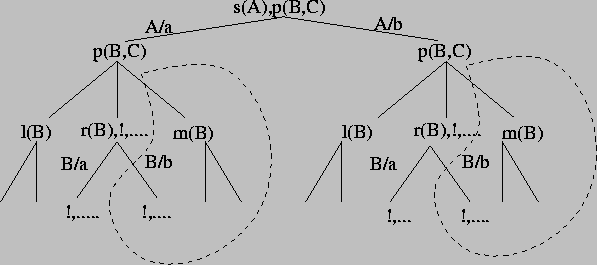
Figure 4.1 shows the effect of the cut in the code below, with the query ?- s(A), p(B, C).:
s(a). p(X,Y):- l(X). s(b). p(X,Y):- r(X),!,..... r(a). p(X,Y):- m(X)........ r(b).
(note the cut in the second clause of p/2). The parts of the tree outlined with a dashed loop are not explored. After traversing the subtree generated by the first clause of p/2 (regardless it has solutions or not, but supposing backtracking is made into the second clause of that predicate), a solution for the call to r/1 is found. Then the cut is executed, which has two effects:
If the predicates after the cut fail, the whole call to p/2 will fail, because the last clause will not be taken into account, nor the second clause of r/1.
Cuts are meta-logical predicates, which have a non-local effect on the computation: in the previous example, the call to r/1 did not respect the usual backtracking semantics, because only one solution is returned, but other calls outside the scope of a cut in the same program would have had a normal behavior: thus, the cut affects the behavior of predicates whose implementation does not imply that.
Cuts, according to the way they affect the program execution, can be divided in several types, regarding their logical safeness, i.e., how much they change (if at all) the logical reading of the program.
max(X,Y,X):- X > Y,!. max(X,Y,Y):- X =< Y.
The two tests are mutually exclusive: since (because of the way arithmetic works in Prolog) both X and Y must be instantiated to numbers, if the first clause succeeds (which will happen if the cut is reached), then the second will not; conversely, if the second clause is to succeed, then the first one could not have succeeded, and the cut in it would not have been reached.
In a CLP language, however, since instantiation of variables is not necessary (the predicate can just constrain and backtrack upon failure), the cut would break the declarative semantics.
For example, if we had a database of addresses of people and their workplaces, and we wanted to know the address of a person, we might prefer his/her home address, and if not found, we should resort to the business address. This predicate implements this query:
address(X, Add):- home_address(X, Add), !. address(X, Add):- business_address(X, Add).
Another useful example is checking if an element is member of a list, without neither enumerating (on backtracking) all the elements of a list nor instantiating on backtracking possible variables in the list. The membercheck/2 predicate does precisely this: when the element sought for is found, the alternative clause which searches in the rest of the list is not taken into account:
membercheck(X, [X|Xs]):- !. membercheck(X, [Y|Xs]):- membercheck(X, Xs).
Again, it might be interesting in some situations, mainly because of the savings in memory and time it helps to achieve. But it should be used with caution, ensuring that it does not remove solutions which are needed.
For example, if we wanted to know how many days there are in a year, taking into account leap years, we might use the following predicate:
days_in_year(X, 366):- number(X), leap_year(X), !. days_in_year(X, 365).
The idea behind is: ``if X is a number and a leap year, then we succeed, and do not need to go to the second clause. Otherwise, it is not a leap year''. But the query ?- leap_year(z, D) succeeds (with D = 365), because the predicate does not take into account that, in any case, a year must be a number. It is arguable that this predicate would behave correctly if it is always called with X instantiated to a number, but the check number(X) would not be needed, and correctness of the predicate will then be completely dependent on the way it is called--which is not a good way of writing predicates.
Another example is the following implementation of the max/3 predicate which works out the maximum of two numbers:
max(X, Y, X):- X > Y, !. max(X, Y, Y).
The idea is: if X > Y, then there is no need to check whether X =< Y or not, hence the cut. And, if the first clause failed, then clearly the case is that X =< Y. But there are two serious counterexamples to this: the first is the query ?- max(5, X, X)., which succeeds binding nothing (instead of failing or giving an error, which would in any case be a better behavior, at least indicating that there has been a call with a wrong instantiation mode).
A possible argument against of this counterexample is that it is violates the supposedly allowed ``call modes'' (i.e., trying to find the maximum of two numbers, one of which is not instantiated), but good programs (logic programs or not) should exhibit a sensible behavior no matter what input is received. In any case, the second counterexample does not violate any sensible assumption: the call ?- max(5, 2, 2). succeeds instead of failing, because the first head unification fails and the second succeeds!
What happens here is a case of the so-called ``output unification'': there are unifications made before the cut, which means that data is changed prior to the tests which determine if the (first, in this case) clause is the right one or not. Changing the program to
max(X, Y, Z):- X > Y, !, X = Z. max(X, Y, Y).
will make the predicate behave correctly in both counterexamples (giving an error in the first, failing in the second).