



Next: Linear (Dis)Equations
Up: Adding Computation Domains
Previous: Adding Computation Domains
A constraint domain introduces new symbols and their associated
semantics in the language. This gives the language an ability to
express computations which go well beyond what was available until
this moment.
While both approaches are equally valid, if the embedding is correctly
made, and fits nicely with the rest of the language, the second is
probably more elegant and leads to languages easier to understand. We
will see that using constraints together with logic programming is
actually a natural step towards a more powerful language.
There is a variety of constraint domains to choose, and CLP languages
choose which one to implement (several at once, in some cases). The
reason for having them is that different problems call for different
constraint domains (due to its nature), and finding the right
constraint domain is usually not difficult. But, in any case, the
first step is deciding a modelization of the problem.
Choosing a constraint domain has another impact: the capabilities of
the solvers for that domain. Not all constraint domains are equally
solvable: some have algorithms which generate a solution (e.g., linear
equations), some need enumeration and trial and error (e.g., finite
domains), and some need an iterative fixpoint-based algorithm which
approximates a solution (e.g., non-linear equations).
Having different constraint systems available is, actually, an
advantage, in that it allows the programmer to model the problem
freely, and then try to adapt (if needed) that model to the constraint
system which more closely resembles the modelization. We will present
some constraint domains which will allow us to perceive the
differences among them, and, at the same time, to understand
how all of them blend easily with the underlying LP machinery.




Next: Linear (Dis)Equations
Up: Adding Computation Domains
Previous: Adding Computation Domains
MCL
1998-12-03
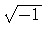 (usually written as
(usually written as 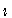 or
or 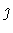 ), and an expanded meaning
for the usual arithmetical operators.
), and an expanded meaning
for the usual arithmetical operators.