Subsections

• Clauses
• Implicit Equality
• Facts
• Predicates
• Programs and Queries

   
A Basic Constraint Language

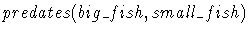
We will define the skeleton of a constraint language, without many interesting capabilities, but which will be enough to understand the principles of constraint programming without the burden of having to cope with unneeded details.

The basic components of our language are the following:

Variables

which hold values throughout the execution. Differently from other languages, variables do not need to be typed or declared anywhere, and so they are distinguished from other elements by their syntax. Variables will always be written starting with an uppercase character: X, Y, Speed.

Constants

which are immutable values. Usual languages can use only numbers as constants, or, at most, a set of predefined strings which make up an enumerated or cardinal type--in fact, this is just another way of assigning names to numbers. Constants are either numbers, including floating point numbers, or names starting with a lowercase character: 87, -45.87, bogus.

Underscores are allowed either in the names of variables or non-numerical constants to improve readability: $Second\_Task$, $a\_dog$.

Atoms

which will play a syntactic rôle similar to procedure definitions and procedure calls. Atoms have the form $p(X_1,\ldots,X_n)$, where p is the name of a procedure or, more strictly, a predicate. X₁ to X_n are the arguments of the atom, and the number of arguments n is termed the arity of p. This is commonly written p/n. Examples of atoms are

hates(dog, cat)

$predates(big\_fish, small\_fish)$

Constraints

which allow writing equations relating variables and constants in the program are written. For now we will use only the constraint = of arity 2, which will denote syntactic equality. We will give examples of their use.

Although constraint languages include builtin atoms which can be used in programs to perform several tasks (e.g., opening and writing to files), this small language will not have them: all the atoms which appear in bodies must be defined by the user somewhere in the program--although they will not always appear explicitly defined in the examples. Conversely, some constraint languages allow the user to define and augment the constraints available, besides those already available in the system, but we will not allow that either at this point.

Clauses

A clause represents a way of achieving a goal. Clauses have the form

$$p \leftarrow b_1, \ldots, b_n.$$ (2.1)

where p is an atom, as defined in the previous section, and $b_1, \ldots, b_n$ are either atoms or constraints. In this expression, pis commonly called the head of the clause, and $b_1, \ldots, b_n$ is called the body. The symbol $\leftarrow$ (which, for typographical convenience, is often written as :-) is called the neck, for it connects the body and the head.

Example 2.1   The following are syntactically correct clauses, as usually written in a computer:

animal(X):- dog = X.
likes(C, F):- C = cat, F = fish.
bigger(M1, M2):- M1 = men, M2 = mice. $\blacksquare$

In this example, animal/1, dog/1, likes/2, and bigger/2 are atoms. X, C, F, M1, M2 are variables, and cat, fish, men, and mice are non-numerical constants. Note that variables and constants can be written on both sides of the equality symbol--it does not matter in which side they appear.

The program has no meaning in itself as it is written, in the same sense that writing x = 3 + y in a conventional language has no meaning other than a mathematical operation whose purpose in the program we do not know. The only a priori possible interpretation comes from the semantics of first order logic: a expression such as that in (2.1) is to be read as for p to be true, $b_1, \ldots, b_n$ have to be true. Then, under an interpretation directed by the names in the code, the example 2.1 can be interpreted as expressing the following:

X is an animal if X equals ``dog'' , or
``dog'' is an animal



``cat'' likes ``fish''



M1 is bigger than M2 if M1 equals ``men'' and M2 equals ``mice'', or
``men'' are bigger than ``mice''

These clauses contained only calls to constraints. Clauses can also refer to other clauses written by the programmer (atoms). The variables in the clauses are used to pass arguments to the atoms in the body (and constants can be passed as well, of course).

Example 2.2   The following clauses have atoms defined by the user in the body:

eats(X, Y):- bigger(X, Y).
pet(X):- animal(X), sound(X,Y), Y=bark. $\blacksquare$

Their reading depends on the interpretation of the user atoms, but a likely meaning of them is:

The big eat the small, or
If some X is bigger than some Y, then X eats Y



For X to be a pet, it must be an animal and the sound it produces must be a bark, or
If X is and animal and X barks, then X is a pet, or
An animal which barks is a pet

Of course, the final answer to the real meaning of this piece of code is what the programmer actually had in mind when writing animal/a, sound/2, and bigger/2.

Implicit Equality

Equality is a very common constraint in all domains, and so it is customary to write it in a shorter form: the clause

p(X):- X = something.

can also be written, with exactly the same meaning as

p(something).

i.e., every time a variable of a clause appears anywhere within a clause, the atom (or variable) this variable is equated to can replace every appearance of that variable.

Example 2.3   The clauses in Example 2.1 can also be written as follows:

bigger(men, mice).
pet(X):- animal(X), sound(X, bark).

and their meaning and behavior is exactly the same as in the original example. $\blacksquare$

   
Facts

The previous section introduced a new type of clause, which is actually a shorthand expression for clauses we already know how to write: the expression

p.

where p is an atom, is called a fact. The first clause in Example 2.3 is a fact, which appears because an equality constraint has been implicitly moved to the head of the clause.

Example 2.4   The first and second clauses in Example 2.1 can also be written as facts:

animal(dog).
likes(cat, fish). $\blacksquare$

Predicates

A predicate is simply a collection of clauses which have the same head name and arity. Recall that the constraints and atoms in the body of a clause represent conditions to be fulfilled in order to achieve a goal--the head--, so they logically represent a conjunction of goals. Different clauses, in turn, represent a disjunction: alternative possibilities to accomplish a target. From a more logical point of view, different clauses of a predicate offer alternative possibilities for the predicate to be true.

Example 2.5   The following predicate expands our idea of what a pet can look like:

pet(X):- animal(X), sound(X, bark).
pet(X):- animal(X), sound(X, bubbles). $\blacksquare$

What is the meaning of this example? In addition to the first, already known clause, which casted animals which bark into the category of pets, we are not including animals whose sound is bubbles (probably fishes) into the very same category. So, in a more colloquial form, the example above can be read as

Animals which bark and animals which make bubbles are pets

Note that when we describe the predicate in a goal-oriented form, the description must take a disjunctive form, closer to the logical meaning of the predicate, but less natural from the point of view of the human language:

For something to be a pet, it must either be an animal and bark, or else be an animal and make bubbles.

Note also that the same variable X appears in both clauses: the names of the variables in a clause are local to that clause, very much like local variables in procedural languages have an scope limited to the procedure/function they are defined in.

Programs and Queries

We are now ready to write programs in our constraint language. A program is simply a collection of predicates, much in the same way that a program in other languages is a collection of procedures or functions.

Example 2.6   The following code implements a program which has knowledge about what is a pet, and, using a database of facts defining some animals and characteristics, infers which animals are (to its knowledge), pets.

  pet(X):- animal(X), sound(X, bark).
  pet(X):- animal(X), sound(X, bubbles).

  animal(spot).
  animal(barry).
  animal(hobbes).

  sound(spot, bark).
  sound(barry, bubbles).
  sound(hobbes, roar).

$\blacksquare$

Since most CLP systems provide an interactive shell for the interpreter / compiler, the user can usually issue commands to load the program, call predicates in it, change the program, and load it again. Calling a predicate from the interpreter yields the same results as calling it from inside a program.

A query issued by the user is just a conjunction of atoms, and has exactly the same form and meaning as the body of a clause. The answer to a query is a set of bindings for the variables which make the query true with respect to the program. Since some predicates may have several clauses which hold for a given query, multiple solutions are possible.

Example 2.7   We will give an example of a possible session with a CLP system. The prompt of the system will be shown as ?-. We will use the program in Example 2.6.

Load the file where the program is stored

?- consult(pet).

Make queries!

?- sound(spot, X).
   X = bark
?- sound(A, roar).
   A = hobbes
?- animal(barry).
   yes
?- animal(X).
   X = spot ;
   X = barry ;
   X = hobbes

$\blacksquare$

Problem 2.1   What will be the answer(s) to the query

?- sound(A, S). $\blacklozenge$