The Munich Rent Advisor
Thom Frühwirth(*), Slim AbdennadherComputer Science Department, University of Munich
Oettingenstr. 67, 80538 Munich, Germany
{Thom.Fruehwirth,Slim.Abdennadher}@informatik.uni-muenchen.de
Computer Science Department, University of Munich
Oettingenstr. 67, 80538 Munich, Germany
{Thom.Fruehwirth,Slim.Abdennadher}@informatik.uni-muenchen.de
Abstract:
Equipped with pencil, paper and calculator, one may need a weekend to figure out the estimated rent. Usually, the calculation is performed by hand in about half on hour by an expert from the City of Munich or from one of the renter's associations. The MS is derived from a statistical model compiled from sample data using statistical methods such as regression analysis [8]. Due to the underlying statistical approach, there is the problem of inherent imprecision which is ignored in the paper version of the MS.
In just two man weeks we developed a computerized prototype called ``The Munich Rent Advisor'', MRA, that brought the advising time down to a few minutes that the user needs to fill in the form. Using constraints the MRA can account for the statistical imprecision and also compute the estimated rent even in the presence of partial answers.
Our approach was to first implement the tables, rules and formulas of the ``Mietspiegel'' with high-level and declarative programming in ECLiPSe [5,6], ECRC's advanced constraint logic programming platform, as if the provided data was precise. Because of the declarativity of ECLiPSe it was easy to express the contents of the MS. Then we added constraints to capture the imprecision due to the statistical method and incompleteness in case the user gives no or partial answers. Finally, we considered the formulas of the rent calculation as constraints that refine the rent estimate by propagation from the constrained input variables. While it would have been difficult to model the required constraints in a given black-box constraints system, it was relatively straightforward using constraint handling rules ( CHRs ). It was enough to modify an existing finite domains solver written in CHRs that is part of the CHR ECLiPSe library. The solver takes just a few pages of code.
The Munich Rent Advisor (MRA) is accessible through the internet, more specifically through World-Wide-Web (WWW). Using the internet, there is no need for the user to acquire specific software.
In about four man-weeks, we wrote the web pages including a form in the Hyper Text Markup Language (HTML). The WWW-front-end is the graphical user-interface that should be handable without experienced computer-knowledge. We chose not to rely on advanced developments like Java applets or frames so that the service is accessible for any internet user. To process the answers from the questionnaire and return its result, we wrote a simple stable special-purpose web-server directly in ECLiPSe using its C-sockets for internet communication.
The paper is organized as follows. The next section introduces the ``Mietspiegel''. Section 3 describes the World-Wide-Web Front End. Section 4 presents the Web-Server in ECLiPSe . Section 5 presents the Munich Rent Advisor from a constraints point of view. Finally, we conclude with a summary and directions for future work.
The scheme for calculating the rent estimate is roughly as follows:
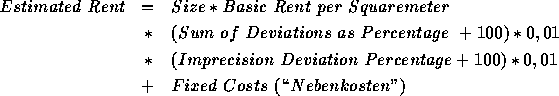
The calculation starts with the average rent per squaremeter taken from a table with about 200 entries. From this anti-monotonic function (the bigger the flat, the less this cost) the average rent is calculated.
The deviations from the average rent are computed from the answers regarding the size, location, features of the flat, as well as age and state of the house. There are six yes-no questions about features of the house concerning e.g. number of floors, optical impression, lift, etc., and 13 yes-no questions about features of the flat concerning e.g. central heating, separate shower, dish-washer, etc. The answers to these questions combined with the age of the house yield the deviations from the average rent.
The main deviation comes from the age of the house, the number of rooms in the flat and if it has a balcony. The overall deviation may be up to 60 percent. It is a non-monotonic function.
For the MS, the complex data-sets derived from the interview have been reduced and simplified so that an average person could calculate the estimated rent. As we have pointed out in the introduction, the MS is still too complicated to be used by everybody. In addition, it ignores the inherent imprecision of the statistical model. The imprecision is basically the standard deviation obtained in the statistical model. Therefore it is higher for rare kinds of flats (very small, big or very old, new etc.). On average, the imprecision deviation amounts to about 10 percent.
Finally one has to add fixed costs (``Nebenkosten'' in German), e.g. taxes, fees for rubbish dump, house cleaning, cable TV and other service charges. Part of them may be included in the rent, part of them not, part of them may not apply. There are currently 16 items on the list of fixed costs. Usually, the user will just ignore this section and thus a range from minimal to maximal fixed costs will be added to the estimated rent. Detailed answers (and thus detailed results) only make sense if the user wants to go to court because he is overcharged with the fixed costs.
Figure 1: Fragment of the Form (compressed postcript, 60K)
For users who are not familiar with the ``Mietspiegel'' (MS) we have created several web pages of background information in German. This is basically plain text with the possibility to go backward, upward and forward in the text. Furthermore, there are the additional possibilities a hypertext document provides: cross-references, links to the city of Munich and renter's associations and to the institutions involved in preparing the MS.
All relevant information for calculating an estimated rent will be collected in the questionnaire. MRA users need to fill in only what they know and what they care about. All answers are optional. There are only four questions requiring numeric inputs, where it is possible to give a range (editable fields) and one question about location requiring a search in a list of districts (pull-down menu). The remaining questions are multiple choices, where the only possible answers are Yes, No and, in addition, Don't know/care (buttons). Optional detailed questions are provided to calculate the fixed costs where numeric input can be given. This form is divided in four sections, basic questions, questions about the house, questions about the flat itself (figure 1) and questions about the fixed costs of the flat. These questions were sorted by importance of the answer to estimate the rent. Questions at the beginning of a section have more influence on the result than questions at the end of a section.
To fit the form on one web-page we had to create a long document that consequently needs a lot of scrolling. We have experimented with internal anchors and links but users found this too complicated. Collecting data from different pages in the server would have been too error-prone:
One problem in implementing the form concerns the flat's location. There are sometimes small areas in the same district that are either extremely expensive or cheap. We tried to use a map just like in the paper version of the MS. There were two problems with this approach. First, in HTML coordinates being extracted out of a map have to be submitted right after they have been taken. So clicking on the map would be possible only at the end of the form as a replacement of the submit-button. But at the end of the document the map is out of context. Second, sending graphical data for a detailed map over a normal connection in the WWW is not acceptable for any user. Obviously, the use of a database that includes street names and numbers with the price level of the rent would be the best solution. Since such database was not available when we implemented the first version of the MRA, we ask only for the main living areas (districts) and otherwise rely on computation with imprecise data using constraints to capture extremes.
To process the answers from the questionnaire and return its result, we wrote a simple stable special-purpose web-server directly in ECLiPSe . This is opposed to the standard approach where for each user request a script is executed (usually written in Perl) via the CGI interface (or using the Unix inetd service). Since starting up ECLiPSe (and ECLiPSe saved states) takes up to a second and considerable memory, it would not have been feasible to start a new ECLiPSe process with each user request. We also did not want to struggle with CGI scripts - but this problem seems to be solved in the meantime [7]. It was more natural that ECLiPSe is constantly running and listening to the port waiting for the next user request. Moreover, this avoids the overhead of using standard Perl-scripts to communicate the data between a standard web server and the ECLiPSe process. The disadvantage is that the server is not concurrent (multi-user). However, since it takes considerably less than a second to serve a user request, we did not encounter problems in practice. We think that the server could be made concurrent (ab)using ECLiPSe 's or-parallelism similar to [11].
ECLiPSe 3.5.x offers a number of built-in predicates for TCP/IP based communication on the internet. The complete socket-library (Internet Protocol Suite) as used under SUN-OS is available. Therefore the basic code of a web-server in ECLiPSe is just:
% top level
go :-
writeln('Starting MRA Server'),
connect(socket),
loop(socket),
close(socket).
% connecting to I/O stream, standard way
connect(Socket) :-
socket(internet,stream,Socket),
bind(Socket, hostname/portnumber)
listen(Socket,1).
% get user requests
loop(S) :-
accept(S,_,IOStream), % get the request
process(IOStream), % process the request
close(IOStream), % done - served the request
loop(S). % go for next request
When the user presses the submit button of the form, the connection will be established ( accept) and the data will be sent to the server. During calculation the connection is in stand-by mode until the result is sent back on the same channel ( IOStream). For calculation, the data is stored temporarily in main memory during the calculation. No personal information is stored. The MRA service is anonymous.
The MRA server only deals with the input posted from the form, all other functionality (e.g. hyperlinks) is provided by a standard server. A general server is available in the recently introduced ECLiPSe http library [4]. However, for real life purposes, this server seems not stable enough: It can hang because it does not use timeouts, and it can fail with browsers because the grammar used for parsing is too strict.
The processing of a user request amounts to the following code:
process(IOStream) :-
readin_request(IOStream,RequestString),
parse(RequestString,InputVarList),
compute(InputVarList,OutputVarList)
->
sendback_result(IOStream,OutputVarList)
;
sendback_error(IOStream).
In readin_request the data is received as an HTML document page (the RequestString) consisting of a header and a body (similar to an e-mail message):
POST / HTTP/1.0 Referer: http://www.ecrc.de/staff/thom/Miet/HTML_SEITEN/miete2.html Connection: Keep-Alive ... Content-type: application/x-www-form-urlencoded Content-length: 654 Language=English&M2_min=22&M2_max=160&ZI_min=1&ZI_max=9& BJ_min=1800&BJ_max=1992&Bezirk=Schwabing& Hinter_Haus=%3F&Guter_Haus_Eindruck=%3F&Renovierung=%3F& ... nk-antenne=0&nk-kabel=8%2C75&nk-kabel=0&nk-summe=350%2C00
Bezirk is German for district, Renovierung means renovation. The message body contains the answers of the user as `` fieldname=value'' entries separated by `` &''.
The difficulty in parsing (predicate parse) is that different browsers may use different syntactic conventions and different encodings for characters (typically codes start with `` %'' followed by a hexadecimal ASCII code).
The fieldnames of the form are associated with Prolog variables which will be used to constrain the input variables:
Language='English', M2_min=22, M2_max=160,... Bezirk='Schwabing',... Renovierung='?',...
In retrospect, using a ground representation (e.g. global variables) or the ECLiPSe library ``structures'' that provides structures with fieldnames would have been easier than passing around a long list of variables.
Then with the predicate compute the estimated rent is computed from the constrained input variables (see next section). This takes less than a second. This means that the Web user gets the reply as fast as loading a medium-sized text-only web page and therefore the pure calculation time is neglectable.
Finally, from the OutputVarList containing the constrained output variables (the main one being the estimated rent), a web page is assembled and sent back to the user (sendback_result) (figure 2).
Figure 2: Result of a Sample Query (compressed postscript, 60K)
If any failure occurs during the processing (connection times out, parsing not possible due to wrong user input in editable fields, computation unexpectedly fails), a generic error message with some hints about typical errors is sent back to the user (sendback_error). Of course, this primitive error handling is only sufficient for a prototype.
From a constraint logic programming point of view [10], the MRA application is quite atypical: The computation proceeds deterministically from constrained input variables (the user data) to constrained output variables (the rent estimate), there is only local search and no backpropagation necessary for the constraints. The reason for this is that the original MS has already solved the problem: It is a complicated function that computes the rent estimate from the user data. When we added constraints to capture imprecise and partial information, this did not change: There is no need for NP-hard constraint solving, only for constraint propagation. Clearly the answer we expect is the smallest interval covering all possible rents, not an enumeration of all possible rents by backtracking.
The MRA implementation is characterized by
Constraint handling rules ( CHRs ) [6,9] are a high-level language extension to write constraint systems. Basically, CHRs are multi-headed guarded rules. CHRs support rapid prototyping of application-oriented constraint systems by providing executable specifications and efficient implementations due to an optimizing compiler. They allow for specialization, modification and combination of constraint solvers.
Simplification CHRs rewrite constraints to simpler constraints while preserving logical equivalence (e.g. X>Y,Y>X <=> false). Propagation CHRs add new constraints which are logically redundant but may cause further simplification (e.g. X>Y,Y>Z ==> X>Z). Repeatedly applying the rules incrementally solves constraints (e.g. A>B,B>C,C>A leads to false). With multiple heads and propagation rules, CHRs provide two features which are essential for non-trivial constraint handling. Due to space limitations, we cannot give a formal account of syntax and semantics of CHRs in this paper.
In the MRA, dealing with imprecise numerical information involves
arithmetic computations with intervals. We modified an existing finite
domain solver in CHRs , domain, that works with arbitrary ground
terms including integers and reals, so that it can deal with interval
constraints over non-linear equations. We first specialized the solver
to interval constraints of the form
X::Min:Max
meaning that X is between Min and Max, which are arbitrary numbers (integers, rationals or floating points). We removed the handling of enumeration domains.
All variables are initialized to their allowed range with such an interval constraint (e.g. the flats covered by the MS are between 22 and 160 squaremeters, i.e. Size::22:160. The fieldname variables are used to constrain the input variables of the MS:
FlatSize::M2_min:M2_max
Boolean truth values are represented by 0 and 1. Boolean variables are initialized as in e.g. Renovierung::0:1. Since we are only interested in the minimal and maximal estimated rent, the approximation of the two boolean values 0 and 1 by the whole interval from 0:1 in case the value is not known does not result in a loss of precision. Using an enumeration domain [0,1] would have been cleaner, but doubled the coding effort for the application-specific constraints.
Furthermore the original CHR solver provides simple inequations and equations ( X=Y, X<Y, X=<Y,...) between two variables or numbers.
The specialized solver contains CHRs like:
X::Min:Min <=> X=Min.
X::Min:Max <=> Min>Max | fail.
X::Min:Max <=> number(X) | Min=<X,X=<Max.
...
Min2 =< X, X::Min1:Max <=> number(Min2) |
maximum(Min1,Min2,Min), X::Min:Max.
...
X =< Y, Y::Min:Max ==> var(X) | X =< Max.
X >= Y, Y::Min:Max ==> var(X) | X >= Min.
CHRs of the form Head <=> Guard | Body (where the guard is optional) are used to simplify the head constraints into the body, provided the guard is satisfied. Similarly, CHRs of the form Head ==> Guard | Body are used to propagate from the head constraints by adding the body. For example, from the constraints A::1:2, B::2:3, A>=B we get A=2,B=2 by applying some of the above CHRs .
Then we extended this simple solver by allowing linear and non-linear equations reducing to the normal form
C0+C1*X1+C2*X2+...+Cn*Xn = Y and C*X1*X2*...*Xn = Y
where the Ci and C are numbers and the Xi and Y are different variables and n>=0. These equations and inequations are needed to express the formulas appearing in the MS. In the implementation, C0+C1*X1+C2*X2+...+Cn*Xn = Y is represented by sum(C0:C0, [C1*X1,C2*X2,...,Cn*Xn], Y)
sum(Min:Max, [], Result) <=> Result::Min:Max.
sum(Min:Max, [C*V|Rest], Result) <=> number(V) |
NewMin is Min + C*V,
NewMax is Max + C*V,
sum(NewMin:NewMax, Rest, Result).
V::VMin:VMax, sum(Min:Max, [C*V|Rest], Result) <=>
NewMin is Min + min(C*VMin,C*VMax),
NewMax is Max + max(C*VMin,C*VMax),
sum(NewMin:NewMax, Rest, Result),
V::VMin:VMax.
Since we do not need backpropagation in our application (as all the formulas compute from the input variables to the output variables which are initially unconstrained), these three rules suffice. The implementation for non-linear equations is as straightforward.
We could presumably have used CLP(BNR) [2] or Newton [3] to express the required constraints. However it would have been quite difficult to tailor the amount and direction of constraint propagation to the needs of the application at hand.
The Mietspiegel contains several tables that relate features of the
flat to percentual changes of the estimated rent. For example, the
rent depends on the age of the flat and its number of rooms. The table
to describe this function as found in the MS is:
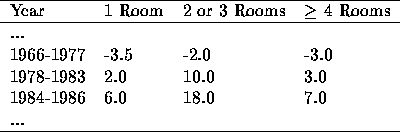
The implementation with interval constraints uses facts of the form table1(YearInterval,RoomsInterval,Percentage). This shorthand maintains readability and saves typing work.
... table1(1966:1977, 1:1, -3.5). table1(1966:1977, 2:3, -2.0). table1(1966:1977, 4:99, -3.0). table1(1978:1983, 1:1, 2.0). table1(1978:1983, 2:3, 10.0). table1(1978:1983, 4:99, 3.0). table1(1984:1986, 1:1, 6.0). table1(1984:1986, 2:3, 18.0). table1(1984:1986, 4:99, 7.0). ...
These table facts are translated
into the corresponding rules of the form
table1(Year,Rooms,Percentage) :-
Year::YearInterval, Rooms::RoomsInterval
at compile time by macro expansion, another useful feature of logic
programming systems.
Overall, the tables of the MS result in several hundred rules.
For example, the query
When we use the tables, we are only interested in the smallest
interval that contains all the answers, not in all answers per se.
The computation is thus deterministic, no choices need to be explored.
This means that we have to collect all the answers and compute minima
and maxima to find the smallest interval that contains all answers.
Instead of a query
table1(Year,Rooms,Percentage)
where we are interested in the interval for Percentage, we use the built-in predicate setof(Variable,Query,List) that collects all bindings of the variable in all the answers to the query in an ordered list.
setof(Percentage,Year^Rooms^table1(Year,Rooms,Percentage),List), first(List,Min), last(List,Max), Percentage::Min:Max.
For example, the above code with Year::1980:1985, Rooms::1:4
yields
Percentage::2.0:18.0.
Note that this code also works if no or just one answer is produced.
A similar procedure was used for all tables. The running time is satisfactory for tables with a few hundred constrained tuples. If the function computed from a table is (anti-)monotonic, the code will be specialized, since then only reasoning on the bounds of the input variables is necessary.
The web-page sent back to the user containing the result is produced by a series of printf calls filling in the actual values or ranges of the variables into a skeleton, e.g. for the header:
printf(IOStream, "<HTML><HEAD><TITLE>%w</TITLE></HEAD><BODY><H1>%w</H1>%b", [Title,Headline])The w-option puts the next element of the list in the third argument into the text written in the second argument. The b-option flushes the output. The tables are produced line by line using a recursion.
It took about 4 man weeks to write the web user interface, only 2 weeks to write the expert system code and 1 week to debug it. We think that the coding would have dominated the implementation effort if a conventional programming language had been used.
The MRA user typically needs only a few minutes to fill in the questionnaire. The calculations of the MRA are performed within a second. This means that the Web user gets the reply as fast as loading a medium-sized text-only web page. Several thousand people haved used our service during a trial phase in winter 95/96.
Our very high-level state-of-the-art approach also means that the program can be easily maintained and modified. This is crucial, since every city and every new version of the "Mietspiegel" comes with different tables and rules.
One direction for future work is to integrate integrity constraints (e.g. if a house is built after 1949, its flats have a bathroom) directly derived from the statistical raw data of the Mietspiegel.
Our application identified the need for lightweight CLP implementations that can run as agents or Java-like applets over the internet. We think that our approach can be applied to many applications where one wants to reason with partial information (e.g. meteorology, mechanics, electrical engineering) without compromising correctness as is the case in ad-hoc ``fuzzification'' approaches.