Constructing Recursive Data Structures

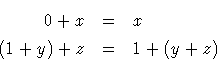
Terms can be used to construct data structures more complex than those we have been using so far. A (simply) recursive data structure is a data structure which has a field which has a structure similar to the initial data structure. The simplest recursive data structure is the so-called Peano numbers. Peano numbers allow the modellization of natural numbers in a simple, homogeneous way, without actually defining different symbols for the digits. Peano numbers are constructed using these two rules:

• z is a Peano number (meaning zero, 0)
• s(N) is a Peano number if N is a Peano number (meaning the successor of N, i.e., N + 1)

The following Peano numbers symbolize what is usually written 0, 1, 2, 3, 4...: z, s(z), s(s(z)), s(s(s(z))), s(s(s(s(z))))...Peano numbers can very easily be defined using terms, as every Peano number is, directly, a first-order term. This code characterizes Peano numbers:

natural(z).
natural(s(N)):- natural(N).

It is interesting to note that this definition is, actually, very similar to the second one given in Section 3.3. Testing for ``zero'' and ``greater than zero'' is automatically made through matching (z does not match s(z), and the same happens the other way around). Subtracting one to continue the recursion is also made implicitly, since when the argument of the predicate matches s(N), N is, by the definition of Peano numbers, the predecessor of s(N). As usual, this allows us to make queries to test and also to generate numbers:

?- natural(z).
   yes

?- natural(potato).
   no

?- natural(s(s(s(z)))).
   yes

?- natural(X).
   X = z ;
   X = s(z) ;
   X = s(s(z));

?- natural(s(s(X))).
   X = z ;
   X = s(z) ;
   X = s(s(z));

All usual integer arithmetic operations can be defined using Peano numbers. For example, below we define the addition of Peano numbers: plus(A, B, C) is true if A plus B equals C, and the three arguments are Peano numbers:

plus(z, X, X):- natural(X).
plus(s(N), X, s(Y)):- plus(N, X, Y).

Note the call to natural/1 in the first clause, to ensure that in fact, the second and third arguments are Peano numbers. plus/3 implements the following two equations:

$$\begin{eqnarray*}0 + x & = & x \\ (1 + y) + z & = & 1 + (y + z) \end{eqnarray*}$$

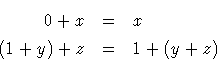
Adding one / subtracting one to a Peano number amounts to putting a functor s/1 around it, or to equate it with s(X), where X is the variable which will be bound to the number minus one. Since this is a logical definition, it can be used with different call modes: it can add, subtract, and decompose a number:

?- plus(s(s(z)), s(z), R).
   R = s(s(s(z)))

?- plus(s(s(s(z))), T, s(s(s(s(s(z))))).
   T = s(z)

?- plus(s(s(s(s(z)))), T, s(s(s(z)))).
   no

?- plus(X, Y, s(s(z))).
   X = z, Y = s(s(z)) ;
   X = s(z), Y = s(z) ;
   X = s(s(z)), Y = z

Problem 3.12   Recall the even/1 program of Section 3.3. Write a version which uses Peano arithmetic. $\blacklozenge$

Problem 3.13   Define the following predicates. All of them should use Peano arithmetic.

• times(X, Y, Z), which is true if X * Y = Z.
• exp(N, X, Y), which is true if Y = X^N.
• factorial(N, F), which is true if F = N!, i.e., $F = 1 * 2 * 3 * \cdots *N$. Note that factorial is commonly defined so that 0! = 1: respect this.
• minimum(A, B, M), which is true if M is the minimum of A and B.
• ltn(X, Y), which is true if X < Y.

$\blacklozenge$

$\mathbf\therefore$

Commonly, predicates can be defined in several ways, all of them logically equivalent, but which may differ greatly in their performance. For example, let us have a look at a couple of definitions of $X \bmod Y$, defined as follows: rem(X, Y, Z) is true if there is an integer Q (for quotient) such that X = Y * Q + Z and Z < Y, i.e., Z is the remainder of the integer division of X by Y. A straightforward translation is as follows:

rem(X, Y, Z):- ltn(Z, Y), times(Y, Q, W), plus(W, Z, X).

which actually works--but quite inefficiently. A typical call with X and Y instantiated to Peano numbers first generates Zs less than Y, and then pairs of numbers Q, W such that Y * Q = W, and after that, it is checked that W + Z = X. A much better (but less direct) implementation is the one below:

rem(X,Y,Z):-
   plus(X1,Y,X),
   rem(X1,Y,Z).
rem(X,Y,X):- ltn(X, Y).

The idea is subtracting Y from X until X is less than Y;^3.3 then X will be the remainder sought for. Note that plus/3 is used to perform a subtraction, and that both clauses are mutually exclusive: if X < Y, then it is not possible that X1 + Y = X (remember that we are dealing with natural numbers). This implementation is much more efficient than the first one, as it does not perform a generate-and-test procedure: it goes straight down to the solution. Also, it does not suffer from the problem of looping in the case of choosing the wrong branch to search, as it was the case of the first implementation for certain calls.