Fibonacci Numbers

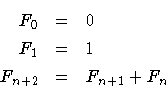
The Fibonacci series is a classical problem in mathematics and computer science. It is usually defined as:

$$\begin{eqnarray*}F_0 & = & 0 \\ F_1 & = & 1 \\ F_{n+2} & = & F_{n+1} + F_n \end{eqnarray*}$$

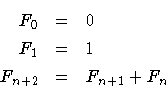
I.e., the numbers of Fibonacci are 0, 1, 1, 2, 3, 5, 8, 13...It is easy to straightforwardly translate it to a logical definition, mimicking each equation with a clause. The first argument of the predicate is the index of the Fibonacci number, and the second argument is the Fibonacci number itself. Note that there is an explicit check of the index in the last clause:

fib(0, 0).
fib(1, 1).
fib(N, F1+F2):-
   gelin(N, 2),
   fib(N-1, F1),
   fib(N-2, F2).

There are two recursive calls in this case. This will be important later. As usual, queries can be issued to find out which number corresponds to a given index:

?- fib(10, F).
   F = 55.

But, as in previous examples, other calls are possible, as, for example, finding out the index of a Fibonacci number:

?- fib(N, 8).
   N = 6

Other interesting queries are possible, as, for example, finding which are the fixpoints of the Fibonacci series (i.e., which numbers are equal to their indexes):

?- fib(N, N).
   N = 0;
   N = 1;
   N = 5

But the above program, having two recursive calls, needs too much memory because of repeated calls: F₁₀₀ needs F₉₉ and F₉₈, but F₉₉ itself needs F₉₈ again, so not only many calls are needed: they are repeated, too. The program can use up the memory allocated for the process in medium sized computations:

?- fib(100, F).
   error: too_many_scols

Increasing the memory allocated by the process only pushes the problem a little bit forward: it is much better to reformulate the program (which, in this case is quite easy) to make another faster (and cheaper in terms of memory) implementation.

Problem 3.8   Write a simply recursive program which defines the Fibonacci series. Hint: use two arguments to store the current Fibonacci number, and the previous one. Find the 1000 ^th Fibonacci number (the last four digits are 8875). $\blacklozenge$