


Next: Finite Domains (I)
Up: Adding Computation Domains: CLP
Previous: Programming with CLP() (I)
-

-
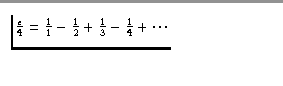 (converges very slowly)
(converges very slowly)
-

- CLP(
 )
program:
)
program:
-
- is_E(N, E4*4):- is_E(N, 1, 1, E4).
is_E(0, Mult, Sign, 0).
is_E(N, Mult, Sign, Sign/Mult + RestE):-
N > 0,
is_E(N-1, Mult+1, -Sign, RestE).
-

- The series added up to the 11
 term:
term:
-
- ?- is_E(11, E).
E = 2.94618
-

- How many terms needed to achieve a given accuracy?
-
- ?- abs(E-E1)<0.01, is_E(N,E), is_E(N+1,E1).
N = 400, E1 = 2.77757, E = 2.76759
-

- abs(E-E1) < 0.01 is delayed and not evaluated until E
and E1 have a known value
-

- Only an example: can be made much more efficiently
Last modification: Thu Oct 7 12:04:03 MEST 1999 <webmaster@clip.dia.fi.upm.es> 

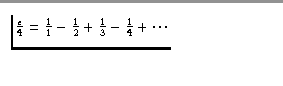 (converges very slowly)
(converges very slowly)