P-99: Ninety-Nine Prolog Problems
Authors: Daniela Ferreiro, Werner Hett (original version)
This is a presentation as an Active Logic Document (ALD) of the Ninety-Nine Prolog Problems written by Werner Hett at the Berne University of Applied Sciences (Switzerland). The original can be found here or here. It has been translated since to many programming languages.
Active Logic Documents such as this one (see also this poster for a quick summary) allow direct interaction with logic programming problems and solutions (editing, testing, issuing queries, etc.) while running everything within your browser. I.e., there is no interaction with a server and your programs run locally in an embedded version of (Ciao) Prolog that requires no installation. The document source is written in a markdown dialect. They are particularly useful, e.g., for teaching Prolog, embedding examples in documentation, manuals, tutorials, etc.
How to use this interactive document:
- The code boxes generally need your interaction. You will identify them by a question mark (?) in the right top corner.
- Your goal is to turn all question marks in such boxes into green checked marks (✔):
- Boxes with a thinking face (🤔) are exercises that you must complete in order to progress. Once an exercise is completed, press the question mark.
- Code errors or failed exercises turn the question mark into a red erroneous mark (✘). You can try again, as many times as you want.
- When available, pressing the northeast pointing arrow (↗) will load the code in a separate Prolog playground window.
- Would you like to test your code? Feel free to submit your answer and make all the queries you want! In each exercise, there is also an editable box with a right-pointing triangle (▶) that allows interaction with the code loaded, by issuing queries. To use these query boxes, make sure the previous code box is checked (✔) (the one with the proposed activity).
Introduction
The purpose of this problem collection is to give you the opportunity to practice your skills in logic programming. Your goal should be to find the most elegant solution of the given problems. Efficiency is important, but logical clarity is even more crucial. Some of the (easy) problems can be trivially solved using built-in predicates. However, in these cases, you learn more if you try to find your own solution.Every predicate that you write should begin with a comment that describes the predicate in a declarative statement. Do not describe procedurally, what the predicate does, but write down a logical statement which includes the arguments of the predicate. You should also indicate the intended data types of the arguments and the allowed flow patterns.
The problems have different levels of difficulty. Those marked with a single asterisk (⭐️) are easy. If you have successfully solved the preceding problems you should be able to solve them within a few (say 15) minutes. Problems marked with two asterisks (⭐️⭐️) are of intermediate difficulty. If you are a skilled Prolog programmer it shouldn't take you more than 30-90 minutes to solve them. Problems marked with three asterisks (⭐️⭐️⭐️) are more difficult. You may need more time (i.e. a few hours or more) to find a good solution.
Working with Prolog lists
A list is either empty or it is composed of a first element (head) and a tail, which is a list itself. In Prolog we represent the empty list by the atom [] and a non-empty list by a term [H|T] where H denotes the head and T denotes the tail.Last element of a list
:- module(_, _, [assertions]).
sorry :- throw(not_solved_yet).
:- test my_last(A, B) : (B = [a,b,c,d])
=> (A = d) + (not_fails, is_det).
%! \begin{hint}
% Example:
% ?- my_last(X,[a,b,c,d]).
% A = d
my_last(X,L) :- sorry.
% X is the last element of the list L
% Note: last(?Elem, ?List) is predefined
%! \end{hint}
%! \begin{solution}
% Example:
% ?- my_last(X,[a,b,c,d]).
% A = d
my_last(X,[X]).
my_last(X,[_|L]) :- my_last(X,L).
%! \end{solution}?- my_last(X,[a,b,c,d]).
Last but one element of a list
:- module(_, _, [assertions]).
sorry :- throw(not_solved_yet).
:- test last_but_one(A, B) : (B = []) + (fails).
:- test last_but_one(A, B) : (B = [1,2,3,4])
=> (A = 3) + (not_fails, is_det).
%! \begin{hint}
% Example:
% ?- last_but_one(X,[1,2,3,4]).
% A = 3
last_but_one(X,L) :- sorry.
% X is the last but one element of the list L
%! \end{hint}
%! \begin{solution}
% Example:
% ?- last_but_one(X,[1,2,3,4]).
% A = 3
last_but_one(X,[X,_]).
last_but_one(X,[_,Y|Ys]) :- last_but_one(X,[Y|Ys]).
%! \end{solution}?- last_but_one(X,[a,b,c,d]).
Find element in a list
:- module(_, _, [assertions]).
sorry :- throw(not_solved_yet).
:- test element_at(A, B, C) : (B = [a,b,c,d,e], C = 3)
=> (A = c) + (not_fails, is_det).
%! \begin{hint}
% Example:
% ?- element_at(X,[a,b,c,d,e],3).
% X = c
element_at(X,L,K) :- sorry.
% X is the K'th element of the list L
% Note: nth1(?Index, ?List, ?Elem) is predefined
%! \end{hint}
%! \begin{solution}
% Example:
% ?- element_at(X,[a,b,c,d,e],3).
% X = c
element_at(X,[X|_],1).
element_at(X,[_|L],K) :- K > 1, K1 is K - 1, element_at(X,L,K1).
%! \end{solution}?- element_at(X,[a,b,c,d,e],3).
Number of elements of a list
:- module(_, _, [assertions]).
sorry :- throw(not_solved_yet).
:- test my_length(A, B) : (A = [1, 4, 5])
=> (B = 3) + (not_fails, is_det).
:- test my_length(A, B) : (A = [])
=> (B = 0) + (not_fails, is_det).
%! \begin{hint}
% Example:
% ?- my_length([1,2,3],X).
% X = 3
my_length(L,N) :- sorry.
% the list L contains N elements
% Note: length(?List, ?Int) is predefined
%! \end{hint}
%! \begin{solution}
% Example:
% ?- my_length([1,2,3],X).
% X = 3
my_length([],0).
my_length([_|L],N) :- my_length(L,N1), N is N1 + 1.
%! \end{solution}?- my_length([1,2,3],X).
Reverse a List
:- module(_, _, [assertions]).
sorry :- throw(not_solved_yet).
:- test my_reverse(A, B) : (A = [1, 4, 5])
=> (B = [5, 4, 1]) + (not_fails, is_det).
:- test my_reverse(A, B) : (A = [a, b, c, d])
=> (B = [d, c, b, a]) + (not_fails, is_det).
%! \begin{hint}
% Example:
% ?- my_reverse([1,4,5],X).
% X = [5,4,1]
my_reverse(L1,L2) :- sorry.
% L2 is the list obtained from L1 by reversing
% the order of the elements.
% Note: reverse(+List1, -List2) is predefined
%! \end{hint}
%! \begin{solution}
% Example:
% ?- my_reverse([1,4,5],X).
% X = [5,4,1]
my_reverse(L1,L2) :- my_rev(L1,L2,[]).
my_rev([],L2,L2) :- !.
my_rev([X|Xs],L2,Acc) :- my_rev(Xs,L2,[X|Acc]).
%! \end{solution}?- my_reverse([1,4,5],X).
Palindrome
:- module(_, _, [assertions]).
:- use_module(library(classic/classic_predicates), [reverse/2]).
sorry :- throw(not_solved_yet).
:- test is_palindrome(A) : (A = [1, 4, 5]) + (fails).
:- test is_palindrome(A) : (A = [1, 2, 3, 2, 1]) + (not_fails).
:- test is_palindrome(A) : (A = []) + (not_fails).
%! \begin{hint}
% Example:
% ?- is_palindrome([x,a,m,a,x]).
% yes
is_palindrome(L) :- sorry.
% L is a palindrome list
%! \end{hint}
%! \begin{solution}
% Example:
% ?- is_palindrome([x,a,m,a,x]).
% yes
is_palindrome(L) :- reverse(L,L).
%! \end{solution}?- is_palindrome([x,a,m,a,x]).
Flatten a list
:- module(_, _, [assertions]).
:- use_module(library(classic/classic_predicates),[append/3]).
sorry :- throw(not_solved_yet).
is_list([]).
is_list([_H|_T]) :- is_list(_T).
:- test my_flatten(A, B) : (A = [a, [b, [c, d], e]])
=> (B = [a, b, c, d, e]) + (not_fails, is_det).
%! \begin{hint}
% Example:
% ?- my_flatten([a, [b, [c, d], e]], X).
% X = [a, b, c, d, e]
my_flatten(L1,L2) :- sorry.
% the list L2 is obtained from the list L1 by
% flattening; i.e. if an element of L1 is a list then it is replaced
% by its elements, recursively.
% Note: flatten(+List1, -List2) is a predefined predicate
%! \end{hint}
%! \begin{solution}
% Example:
% ?- my_flatten([a, [b, [c, d], e]], X).
% X = [a, b, c, d, e]
my_flatten(X,[X]) :- \+ is_list(X).
my_flatten([],[]).
my_flatten([X|Xs],Zs) :- my_flatten(X,Y), my_flatten(Xs,Ys), append(Y,Ys,Zs).
%! \end{solution}?- my_flatten([a, [b, [c, d], e]], X).
Eliminate duplicates
:- module(_, _, [assertions]).
sorry :- throw(not_solved_yet).
:- test compress(A, B) : (A = [1,1,1,2,2,3,2,2,2])
=> (B = [1,2,3,2]) + (not_fails, is_det).
:- test compress(A, B) : (A = [])
=> (B = []) + (not_fails, is_det).
%! \begin{hint}
% Example:
% ?- compress([a,a,a,a,b,c,c,a,a,d,e,e,e,e],X).
% X = [a,b,c,a,d,e]
compress(L1,L2) :- sorry.
% the list L2 is obtained from the list L1 by
% compressing repeated occurrences of elements into a single copy
% of the element.
%! \end{hint}
%! \begin{solution}
% Example:
% ?- compress([a,a,a,a,b,c,c,a,a,d,e,e,e,e],X).
% X = [a,b,c,a,d,e]
compress([],[]).
compress([X],[X]).
compress([X,X|Xs],Zs) :-
compress([X|Xs],Zs).
compress([X,Y|Ys],[X|Zs]) :-
X \= Y,
compress([Y|Ys],Zs).
%! \end{solution}?- compress([a,a,a,a,b,c,c,a,a,d,e,e,e,e],X).
Pack consecutive duplicates
:- module(_, _, [assertions]).
sorry :- throw(not_solved_yet).
:- test pack(A, B) : (A = [a,a,a,a,b,c,c,a,a,d,e,e,e,e])
=> (B = [[a,a,a,a],[b],[c,c],[a,a],[d],[e,e,e,e]]) + (not_fails, is_det).
:- test pack(A, B) : (A = [1])
=> (B = [[1]]) + (not_fails, is_det).
%! \begin{hint}
% Example:
% ?- pack([a,a,a,a,b,c,c,a,a,d,e,e,e,e],X).
% X = [[a,a,a,a],[b],[c,c],[a,a],[d],[e,e,e,e]]
pack(L1,L2) :- sorry.
% the list L2 is obtained from the list L1 by packing
% repeated occurrences of elements into separate sublists.
% (list,list) (+,?)
%! \end{hint}
%! \begin{solution}
% Example:
% ?- pack([a,a,a,a,b,c,c,a,a,d,e,e,e,e],X).
% X = [[a,a,a,a],[b],[c,c],[a,a],[d],[e,e,e,e]]
pack([],[]).
pack([X|Xs],[Z|Zs]) :- transfer(X,Xs,Ys,Z), pack(Ys,Zs).
% transfer(X,Xs,Ys,Z) Ys is the list that remains from the list Xs
% when all leading copies of X are removed and transfered to Z
transfer(X,[],[],[X]).
transfer(X,[Y|Ys],[Y|Ys],[X]) :- X \= Y.
transfer(X,[X|Xs],Ys,[X|Zs]) :- transfer(X,Xs,Ys,Zs).
%! \end{solution}?- pack([a,a,a,a,b,c,c,a,a,d,e,e,e,e],X).
Run-length encoding
:- module(_, _, [assertions]).
:- use_module(library(classic/classic_predicates),[length/2]).
sorry :- throw(not_solved_yet).
:- test encode(A, B) : (A = [a,a,a,a,b,c,c,a,a,d,e,e,e,e])
=> (B = [[4,a],[1,b],[2,c],[2,a],[1,d],[4,e]]) + (not_fails, is_det).
:- test encode(A, B) : (A = [1,1,1])
=> (B = [[3,1]]) + (not_fails, is_det).
:- test encode(A, B) : (A = [])
=> (B = []) + (not_fails, is_det).
pack([],[]).
pack([X|Xs],[Z|Zs]) :- transfer(X,Xs,Ys,Z), pack(Ys,Zs).
transfer(X,[],[],[X]).
transfer(X,[Y|Ys],[Y|Ys],[X]) :- X \= Y.
transfer(X,[X|Xs],Ys,[X|Zs]) :- transfer(X,Xs,Ys,Zs).
%! \begin{hint}
% Example:
% ?- encode([a,a,a,a,b,c,c,a,a,d,e,e,e,e],X).
% X = [[4,a],[1,b],[2,c],[2,a],[1,d],[4,e]]
encode(L1,L2) :- sorry.
% the list L2 is obtained from the list L1 by run-length
% encoding. Consecutive duplicates of elements are encoded as terms [N,E],
% where N is the number of duplicates of the element E.
% (list,list) (+,?)
%! \end{hint}
%! \begin{solution}
% Example:
% ?- encode([a,a,a,a,b,c,c,a,a,d,e,e,e,e],X).
% X = [[4,a],[1,b],[2,c],[2,a],[1,d],[4,e]]
encode(L1,L2) :- pack(L1,L), transform(L,L2).
transform([],[]).
transform([[X|Xs]|Ys],[[N,X]|Zs]) :- length([X|Xs],N), transform(Ys,Zs).
%! \end{solution}?- encode([a,a,a,a,b,c,c,a,a,d,e,e,e,e],X).
:- module(_, _, [assertions]).
:- use_module(library(classic/classic_predicates),[length/2]).
sorry :- throw(not_solved_yet).
:- test encode_modified(A, B) : (A = [a,a,a,a,b,c,c,a,a,d,e,e,e,e])
=> (B = [[4,a],b,[2,c],[2,a],d,[4,e]]) + (not_fails, is_det).
:- test encode_modified(A, B) : (A = [1,1,1])
=> (B = [[3,1]]) + (not_fails, is_det).
:- test encode_modified(A, B) : (A = [])
=> (B = []) + (not_fails, is_det).
pack([],[]).
pack([X|Xs],[Z|Zs]) :- transfer(X,Xs,Ys,Z), pack(Ys,Zs).
transfer(X,[],[],[X]).
transfer(X,[Y|Ys],[Y|Ys],[X]) :- X \= Y.
transfer(X,[X|Xs],Ys,[X|Zs]) :- transfer(X,Xs,Ys,Zs).
encode(L1,L2) :- pack(L1,L), transform(L,L2).
transform([],[]).
transform([[X|Xs]|Ys],[[N,X]|Zs]) :- length([X|Xs],N), transform(Ys,Zs).
%! \begin{hint}
% Example
% ?- encode_modified([a,a,a,a,b,c,c,a,a,d,e,e,e,e],X).
% X = [[4,a],b,[2,c],[2,a],d,[4,e]]
encode_modified(L1,L2) :- sorry.
% the list L2 is obtained from the list L1 by
% run-length encoding. Consecutive duplicates of elements are encoded
% as terms [N,E], where N is the number of duplicates of the element E.
% However, if N equals 1 then the element is simply copied into the
% output list.
% (list,list) (+,?)
%! \end{hint}
%! \begin{solution}
% Example
% ?- encode_modified([a,a,a,a,b,c,c,a,a,d,e,e,e,e],X).
% X = [[4,a],b,[2,c],[2,a],d,[4,e]]
encode_modified(L1,L2) :- encode(L1,L), strip(L,L2).
strip([],[]).
strip([[1,X]|Ys],[X|Zs]) :- strip(Ys,Zs).
strip([[N,X]|Ys],[[N,X]|Zs]) :- N > 1, strip(Ys,Zs).
%! \end{solution}?- encode_modified([a,a,a,a,b,c,c,a,a,d,e,e,e,e],X).
:- module(_, _, [assertions]).
sorry :- throw(not_solved_yet).
:- test encode_direct(A, B) : (A = [a,a,a,a,b,c,c,a,a,d,e,e,e,e])
=> (B = [[4,a],b,[2,c],[2,a],d,[4,e]]) + (not_fails, is_det).
%! \begin{hint}
% Example:
% ?- encode_direct([a,a,a,a,b,c,c,a,a,d,e,e,e,e],X).
% X = [[4,a],b,[2,c],[2,a],d,[4,e]]
encode_direct(L1,L2) :- sorry.
% the list L2 is obtained from the list L1 by
% run-length encoding. Consecutive duplicates of elements are encoded
% as terms [N,E], where N is the number of duplicates of the element E.
% However, if N equals 1 then the element is simply copied into the
% output list.
% (list,list) (+,?)
%! \end{hint}
%! \begin{solution}
% Example:
% ?- encode_direct([a,a,a,a,b,c,c,a,a,d,e,e,e,e],X).
% X = [[4,a],b,[2,c],[2,a],d,[4,e]]
encode_direct([],[]).
encode_direct([X|Xs],[Z|Zs]) :- count(X,Xs,Ys,1,Z), encode_direct(Ys,Zs).
% count(X,Xs,Ys,K,T) Ys is the list that remains from the list Xs
% when all leading copies of X are removed. T is the term [N,X],
% where N is K plus the number of X's that can be removed from Xs.
% In the case of N=1, T is X, instead of the term [1,X].
count(X,[],[],1,X).
count(X,[],[],N,[N,X]) :- N > 1.
count(X,[Y|Ys],[Y|Ys],1,X) :- X \= Y.
count(X,[Y|Ys],[Y|Ys],N,[N,X]) :- N > 1, X \= Y.
count(X,[X|Xs],Ys,K,T) :- K1 is K + 1, count(X,Xs,Ys,K1,T).
%! \end{solution}?- encode_direct([a,a,a,a,b,c,c,a,a,d,e,e,e,e],X).
Run-length decoding
:- module(_, _, [assertions]).
sorry :- throw(not_solved_yet).
:- test decode(A, B) : (A = [[4,a],b,[2,c],[2,a],d,[4,e]])
=> (B = [a,a,a,a,b,c,c,a,a,d,e,e,e,e]) + (not_fails, is_det).
:- test decode(A, B) : (A = [[3,1]])
=> (B = [1,1,1]) + (not_fails, is_det).
:- test decode(A, B) : (A = [])
=> (B = []) + (not_fails, is_det).
is_list([]).
is_list([_H|_T]) :- is_list(_T).
%! \begin{hint}
% Example
% ?- decode([[4,a],b,[2,c],[2,a],d,[4,e]],X).
% X = [a,a,a,a,b,c,c,a,a,d,e,e,e,e]
decode(L1,L2) :- sorry.
% L2 is the uncompressed version of the run-length
% encoded list L1.
% (list,list) (+,?)
%! \end{hint}
%! \begin{solution}
% Example
% ?- decode([[4,a],b,[2,c],[2,a],d,[4,e]],X).
% X = [a,a,a,a,b,c,c,a,a,d,e,e,e,e]
decode([],[]).
decode([X|Ys],[X|Zs]) :- \+ is_list(X), decode(Ys,Zs).
decode([[1,X]|Ys],[X|Zs]) :- decode(Ys,Zs).
decode([[N,X]|Ys],[X|Zs]) :- N > 1, N1 is N - 1, decode([[N1,X]|Ys],Zs).
%! \end{solution}?- decode([[4,a],b,[2,c],[2,a],d,[4,e]],X).
Duplicate the Elements of a List
:- module(_, _, [assertions]).
sorry :- throw(not_solved_yet).
:- test dupli(A, B) : (A = [a,b,c,c,d]) => (B = [a,a,b,b,c,c,c,c,d,d]) + (not_fails, is_det).
:- test dupli(A, B) : (A = []) => (B = []) + (not_fails, is_det).
%! \begin{hint}
% Example:
% ?- dupli([a,b,c,c,d],X).
% X = [a,a,b,b,c,c,c,c,d,d]
dupli(L1,L2) :- sorry.
% L2 is obtained from L1 by duplicating all elements.
% (list,list) (?,?)
%! \end{hint}
%! \begin{solution}
% Example:
% ?- dupli([a,b,c,c,d],X).
% X = [a,a,b,b,c,c,c,c,d,d]
dupli([],[]).
dupli([X|Xs],[X,X|Ys]) :- dupli(Xs,Ys).
%! \end{solution} ?- dupli([a,b,c,c,d],X).
Duplicate the elements of a list a given number of times
:- module(_, _, [assertions]).
:- push_prolog_flag(multi_arity_warnings, off).
sorry :- throw(not_solved_yet).
:- test dupli(A, B, C) : (A = [a,b,c], B = 3) => (C = [a,a,a,b,b,b,c,c,c]) + (not_fails, is_det).
:- test dupli(A, _B, C) : (A = []) => (C = []) + (not_fails, is_det).
%! \begin{hint}
% Example:
% ?- dupli([a,b,c],3,X).
% X = [a,a,a,b,b,b,c,c,c]
dupli(L1,N,L2) :- sorry.
% L2 is obtained from L1 by duplicating all elements
% N times.
% (list,integer,list) (?,+,?)
dupli(L1,N,L2,K) :- sorry.
% L2 is obtained from L1 by duplicating its leading
% element K times, all other elements N times.
%(list,integer,list,integer) (?,+,?,+)
%! \end{hint}
%! \begin{solution}
% Example:
% ?- dupli([a,b,c],3,X).
% X = [a,a,a,b,b,b,c,c,c]
dupli(L1,N,L2) :- dupli(L1,N,L2,N).
dupli([],_,[],_).
dupli([_|Xs],N,Ys,0) :- dupli(Xs,N,Ys,N).
dupli([X|Xs],N,[X|Ys],K) :- K > 0, K1 is K - 1, dupli([X|Xs],N,Ys,K1).
%! \end{solution} ?- dupli(X,3,Y).
Drop every N'th element from a list.
:- module(_, _, [assertions]).
:- push_prolog_flag(multi_arity_warnings, off).
sorry :- throw(not_solved_yet).
:- test drop(A, B, C) : (A = [a,b,c,d,e,f,g,h,i,k], B = 3) => (C = [a,b,d,e,g,h,k]) + (not_fails, is_det).
:- test drop(A, _B, C) : (A = []) => (C = []) + (not_fails, is_det).
%! \begin{hint}
% Example:
% ?- drop([a,b,c,d,e,f,g,h,i,k],3,X).
% X = [a,b,d,e,g,h,k]
drop(L1,N,L2) :- sorry.
% L2 is obtained from L1 by dropping every N'th element.
% (list,integer,list) (?,+,?)
drop(L1,N,L2,K) :- sorry.
% L2 is obtained from L1 by first copying K-1 elements
% and then dropping an element and, from then on, dropping every
% N'th element.
% (list,integer,list,integer) (?,+,?,+)
%! \end{hint}
%! \begin{solution}
% Example:
% ?- drop([a,b,c,d,e,f,g,h,i,k],3,X).
% X = [a,b,d,e,g,h,k]
drop(L1,N,L2) :- drop(L1,N,L2,N).
drop([],_,[],_).
drop([_|Xs],N,Ys,1) :- drop(Xs,N,Ys,N).
drop([X|Xs],N,[X|Ys],K) :- K > 1, K1 is K - 1, drop(Xs,N,Ys,K1).
%! \end{solution} ?- drop([a,b,c,d,e,f,g,h,i,k],3,X).
Split a list
:- module(_, _, [assertions]).
sorry :- throw(not_solved_yet).
:- test split(A, B, C, D) : (A = [a,b,c,d,e,f,g,h,i,k], B = 3) => (C = [a,b,c], D = [d,e,f,g,h,i,k]) + (not_fails, is_det).
:- test split(A, B, C, D) : (A = [1,2,3], B = 0) => ( C = [], D = [1,2,3]) + (not_fails, is_det).
%! \begin{hint}
% Example:
% ?- split([a,b,c,d,e,f,g,h,i,k],3,L1,L2).
% L1 = [a,b,c]
% L2 = [d,e,f,g,h,i,k]
split(L,N,L1,L2) :- sorry.
% the list L1 contains the first N elements
% of the list L, the list L2 contains the remaining elements.
% (list,integer,list,list) (?,+,?,?)
%! \end{hint}
%! \begin{solution}
% Example:
% ?- split([a,b,c,d,e,f,g,h,i,k],3,L1,L2).
% L1 = [a,b,c]
% L2 = [d,e,f,g,h,i,k]
split(L,0,[],L).
split([X|Xs],N,[X|Ys],Zs) :- N > 0, N1 is N - 1, split(Xs,N1,Ys,Zs).
%! \end{solution} ?- split([a,b,c,d,e,f,g,h,i,k],3,L1,L2).
Extract a slice from a list
:- module(_, _, [assertions]).
sorry :- throw(not_solved_yet).
:- test slice(A, B, C, D) : (A = [a,b,c,d,e,f,g,h,i,k], B = 3, C = 7) =>
(D = [c,d,e,f,g]) + (not_fails, is_det).
:- test slice(A, B, C, D) : (A = [1,2,3], B = 1, C = 1) => (D = [1]) + (not_fails, is_det).
%! \begin{hint}
% Example:
% ?- slice([a,b,c,d,e,f,g,h,i,k],3,7,L).
% X = [c,d,e,f,g]
slice(L1,I,K,L2) :- sorry.
% L2 is the list of the elements of L1 between
% index I and index K (both included).
% (list,integer,integer,list) (?,+,+,?)
%! \end{hint}
%! \begin{solution}
% Example:
% ?- slice([a,b,c,d,e,f,g,h,i,k],3,7,L).
% X = [c,d,e,f,g]
slice([X|_],1,1,[X]).
slice([X|Xs],1,K,[X|Ys]) :- K > 1,
K1 is K - 1, slice(Xs,1,K1,Ys).
slice([_|Xs],I,K,Ys) :- I > 1,
I1 is I - 1, K1 is K - 1, slice(Xs,I1,K1,Ys).
%! \end{solution} ?- slice([a,b,c,d,e,f,g,h,i,k],3,7,L).
Rotate a list
:- module(_, _, [assertions]).
:- use_module(library(classic/classic_predicates),[length/2, append/3]).
sorry :- throw(not_solved_yet).
:- test rotate(A, B, C) : (A = [a,b,c,d,e,f,g,h], B = 3)
=> (C = [d,e,f,g,h,a,b,c]) + (not_fails, is_det).
:- test rotate(A, B, C) : (A = [a,b,c,d,e,f,g,h], B = -2)
=> (C = [g,h,a,b,c,d,e,f]) + (not_fails, is_det).
:- test rotate(A, B, C) : (A = [a,b,c,d,e,f,g,h], B = 0)
=> (C = [a,b,c,d,e,f,g,h]) + (not_fails, is_det).
split(L,0,[],L).
split([X|Xs],N,[X|Ys],Zs) :- N > 0, N1 is N - 1, split(Xs,N1,Ys,Zs).
%! \begin{hint}
% Example:
% ?- rotate([a,b,c,d,e,f,g,h],3,X).
% X = [d,e,f,g,h,a,b,c]
rotate(L1,N,L2) :- sorry.
% the list L2 is obtained from the list L1 by
% rotating the elements of L1 N places to the left.
% (list,integer,list) (+,+,?)
%! \end{hint}
%! \begin{solution}
% Example:
% ?- rotate([a,b,c,d,e,f,g,h],3,X).
% X = [d,e,f,g,h,a,b,c]
rotate(L1,N,L2) :- N >= 0,
length(L1,NL1), N1 is N mod NL1, rotate_left(L1,N1,L2).
rotate(L1,N,L2) :- N < 0,
length(L1,NL1), N1 is NL1 + N, rotate_left(L1,N1,L2).
rotate_left(L,0,L).
rotate_left(L1,N,L2) :- N > 0, split(L1,N,S1,S2), append(S2,S1,L2).
%! \end{solution} ?- rotate([a,b,c,d,e,f,g,h],-2,X).
Remove an element from a list
:- module(_, _, [assertions]).
sorry :- throw(not_solved_yet).
:- test remove_at(A, B, C, D) : (B = [a,b,c,d], C = 2)
=> (A = b, D = [a,c,d]) + (not_fails, is_det).
:- test remove_at(A, B, C, D) : (B = [a,b,c,d], C = 1)
=> (A = a, D = [b,c,d]) + (not_fails, is_det).
%! \begin{hint}
% Example:
% ?- remove_at(X,[a,b,c,d],2,R).
% X = b
% R = [a,c,d]
remove_at(X,L,K,R) :- sorry.
% X is the K'th element of the list L; R is the
% list that remains when the K'th element is removed from L.
% (element,list,integer,list) (?,?,+,?)
%! \end{hint}
%! \begin{solution}
% Example:
% ?- remove_at(X,[a,b,c,d],2,R).
% X = b
% R = [a,c,d]
remove_at(X,[X|Xs],1,Xs).
remove_at(X,[Y|Xs],K,[Y|Ys]) :-
K > 1,
K1 is K - 1,
remove_at(X,Xs,K1,Ys).
%! \end{solution} ?- remove_at(X,[a,b,c,d],2,R).
Insert an element into a list
:- module(_, _, [assertions]).
sorry :- throw(not_solved_yet).
remove_at(X,[X|Xs],1,Xs).
remove_at(X,[Y|Xs],K,[Y|Ys]) :-
K > 1,
K1 is K - 1,
remove_at(X,Xs,K1,Ys).
:- test insert_at(A, B, C, D) : (A = alfa, B = [a,b,c,d], C = 2)
=> (D = [a,alfa,b,c,d]) + (not_fails, is_det).
:- test insert_at(A, B, C, D) : (A = alfa, B = [a,b,c,d], C = 1)
=> (D = [alfa,a,b,c,d]) + (not_fails, is_det).
:- test insert_at(A, B, C, D) : (A = alfa, B = [a,b,c,d], C = 6) + fails.
%! \begin{hint}
% Example:
% ?- insert_at(alfa,[a,b,c,d],2,L).
% L = [a,alfa,b,c,d]
insert_at(X,L,K,R) :- sorry.
% X is inserted into the list L such that it
% occupies position K. The result is the list R.
% (element,list,integer,list) (?,?,+,?)
%! \end{hint}
%! \begin{solution}
% Example:
% ?- insert_at(alfa,[a,b,c,d],2,L).
% L = [a,alfa,b,c,d]
insert_at(X,L,K,R) :- remove_at(X,R,K,L).
%! \end{solution} ?- insert_at(alfa,[a,b,c,d],2,L).
Creating lists
:- module(_, _, [assertions]).
sorry :- throw(not_solved_yet).
:- test range(A, B, C) : (A = 4, B = 9)
=> (C = [4,5,6,7,8,9]) + (not_fails, is_det).
:- test range(A, B, C) : (A = 3, B = 3)
=> (C = [3]) + (not_fails, is_det).
:- test range(A, B, C) : (A = 3, B = 2) + fails.
%! \begin{hint}
% Example:
% ?- range(4,9,L).
% L = [4,5,6,7,8,9]
range(I,K,L) :- sorry.
% I <= K, and L is the list containing all
% consecutive integers from I to K.
% (integer,integer,list) (+,+,?)
%! \end{hint}
%! \begin{solution}
% Example:
% ?- range(4,9,L).
% L = [4,5,6,7,8,9]
range(I,I,[I]).
range(I,K,[I|L]) :- I < K, I1 is I + 1, range(I1,K,L).
%! \end{solution} ?- range(4,9,L).
Generate combinations
:- module(_, _, [assertions]).
sorry :- throw(not_solved_yet).
%! \begin{hint}
% Example:
% ?- combination(3,[a,b,c,d,e,f],L).
% L = [a,b,c] ;
% L = [a,b,d] ;
% L = [a,b,e] ;
% ...
combination(K,L,C) :- sorry.
% C is a list of K distinct elements
% chosen from the list L
%! \end{hint}
%! \begin{solution}
% Example:
% ?- combination(3,[a,b,c,d,e,f],L).
% L = [a,b,c] ;
% L = [a,b,d] ;
% L = [a,b,e] ;
% ...
combination(0,_,[]).
combination(K,L,[X|Xs]) :- K > 0,
el(X,L,R), K1 is K-1, combination(K1,R,Xs).
% Find out what the following predicate el/3 exactly does.
el(X,[X|L],L).
el(X,[_|L],R) :- el(X,L,R).
%! \end{solution} ?- combination(3,[a,b,c,d,e,f],L).
Grouping elements of a list
:- module(_, _, [assertions]).
:- use_module(library(idlists), [subtract/3]).
sorry :- throw(not_solved_yet).
%! \begin{hint}
% Example:
% ?- group3([aldo,beat,carla,david,evi,flip,gary,hugo,ida],G1,G2,G3).
% G1 = [aldo,beat], G2 = [carla,david,evi], G3 = [flip,gary,hugo,ida]
% ...
group3(G,G1,G2,G3) :- sorry.
% distribute the 9 elements of G into G1, G2, and G3,
% such that G1, G2 and G3 contain 2,3 and 4 elements respectively
selectN(N,L,S) :- sorry.
% select N elements of the list L and put them in
% the set S. Via backtracking return all possible selections, but
% avoid permutations; i.e. after generating S = [a,b,c] do not return
% S = [b,a,c], etc.
%! \end{hint}
%! \begin{solution}
% Example:
% ?- group3([aldo,beat,carla,david,evi,flip,gary,hugo,ida],G1,G2,G3).
% G1 = [aldo,beat], G2 = [carla,david,evi], G3 = [flip,gary,hugo,ida]
% ...
group3(G,G1,G2,G3) :-
selectN(2,G,G1),
subtract(G,G1,R1),
selectN(3,R1,G2),
subtract(R1,G2,R2),
selectN(4,R2,G3),
subtract(R2,G3,[]).
selectN(0,_,[]) :- !.
selectN(N,L,[X|S]) :- N > 0,
el(X,L,R),
N1 is N-1,
selectN(N1,R,S).
el(X,[X|L],L).
el(X,[_|L],R) :- el(X,L,R).
%! \end{solution} ?- group3([aldo,beat,carla,david,evi,flip,gary,hugo,ida],G1,G2,G3).
:- module(_, _, [assertions]).
:- use_module(library(idlists), [subtract/3]).
sorry :- throw(not_solved_yet).
%! \begin{hint}
% Example:
% ?- group([aldo,beat,carla,david,evi,flip,gary,hugo,ida],[2,2,5],Gs).
% Gs = [[aldo,beat],[carla,david],[evi,flip,gary,hugo,ida]]
% ...
group(G,Ns,Gs) :- sorry.
% distribute the elements of G into the groups Gs.
% The group sizes are given in the list Ns.
%! \end{hint}
%! \begin{solution}
% Example:
% ?- group([aldo,beat,carla,david,evi,flip,gary,hugo,ida],[2,2,5],Gs).
% Gs = [[aldo,beat],[carla,david],[evi,flip,gary,hugo,ida]]
% ...
group([],[],[]).
group(G,[N1|Ns],[G1|Gs]) :-
selectN(N1,G,G1),
subtract(G,G1,R),
group(R,Ns,Gs).
%! \end{solution} ?- group([aldo,beat,carla,david,evi,flip,gary,hugo,ida],[2,2,5],Gs).
Note that we do not want permutations of the group members; i.e. [[aldo,beat],...] is the same solution as [[beat,aldo],...]. However, we make a difference between [[aldo,beat],[carla,david],...] and [[carla,david],[aldo,beat],...].
You may find more about this combinatorial problem in a good book on discrete mathematics under the term "multinomial coefficients".
Sort a list of lists
:- module(_, _, [assertions]).
:- push_prolog_flag(multi_arity_warnings, off).
:- use_module(library(classic/classic_predicates), [keysort/2]).
:- use_module(library(classic/classic_predicates), [length/2]).
sorry :- throw(not_solved_yet).
:- test lsort(A,B) : (A = [[a,b,c],[d,e],[f,g,h],[d,e],[i,j,k,l],[m,n],[o]])
=> (B = [[o], [d, e], [d, e], [m, n], [a, b, c], [f, g, h], [i, j, k, l]]) + (not_fails, is_det).
%! \begin{hint}
% Example:
% ?- lsort([[a,b,c],[d,e],[f,g,h],[d,e],[i,j,k,l],[m,n],[o]],L).
% L = [[o], [d, e], [d, e], [m, n], [a, b, c], [f, g, h], [i, j, k, l]]
lsort(InList,OutList) :- sorry.
% it is supposed that the elements of InList
% are lists themselves. Then OutList is obtained from InList by sorting
% its elements according to their length. lsort/2 sorts ascendingly,
% lsort/3 allows for ascending or descending sorts.
% (list_of_lists,list_of_lists), (+,?)
%! \end{hint}
%! \begin{solution}
% Example:
% ?- lsort([[a,b,c],[d,e],[f,g,h],[d,e],[i,j,k,l],[m,n],[o]],L).
% L = [[o], [d, e], [d, e], [m, n], [a, b, c], [f, g, h], [i, j, k, l]]
lsort(InList,OutList) :- lsort(InList,OutList,asc).
% sorting direction Dir is either asc or desc
lsort(InList,OutList,Dir) :-
add_key(InList,KList,Dir),
keysort(KList,SKList),
rem_key(SKList,OutList).
add_key([],[],_).
add_key([X|Xs],[L-p(X)|Ys],asc) :- !,
length(X,L), add_key(Xs,Ys,asc).
add_key([X|Xs],[L-p(X)|Ys],desc) :-
length(X,L1), L is -L1, add_key(Xs,Ys,desc).
rem_key([],[]).
rem_key([_-p(X)|Xs],[X|Ys]) :- rem_key(Xs,Ys).
%! \end{solution} ?- lsort([[a,b,c],[d,e],[f,g,h],[d,e],[i,j,k,l],[m,n],[o]],L).
:- module(_, _, [assertions]).
:- push_prolog_flag(multi_arity_warnings, off).
:- use_module(library(classic/classic_predicates), [keysort/2]).
:- use_module(library(classic/classic_predicates), [length/2]).
:- use_module(library(llists), [flatten/2]).
sorry :- throw(not_solved_yet).
lsort(InList,OutList,Dir) :-
add_key(InList,KList,Dir),
keysort(KList,SKList),
rem_key(SKList,OutList).
add_key([],[],_).
add_key([X|Xs],[L-p(X)|Ys],asc) :- !,
length(X,L), add_key(Xs,Ys,asc).
add_key([X|Xs],[L-p(X)|Ys],desc) :-
length(X,L1), L is -L1, add_key(Xs,Ys,desc).
rem_key([],[]).
rem_key([_-p(X)|Xs],[X|Ys]) :- rem_key(Xs,Ys).
:- test lfsort(A,B) : (A = [[a,b,c],[d,e],[f,g,h],[d,e],[i,j,k,l],[m,n],[o]])
=> (B = [[i, j, k, l], [o], [a, b, c], [f, g, h], [d, e], [d,e], [m, n]]) + (not_fails, is_det).
%! \begin{hint}
% Example:
% ?- lfsort([[a,b,c],[d,e],[f,g,h],[d,e],[i,j,k,l],[m,n],[o]],L).
% L = [[i, j, k, l], [o], [a, b, c], [f, g, h], [d, e], [d,e], [m, n]]
lfsort(InList,OutList) :- sorry.
% it is supposed that the elements of InList
% are lists themselves. Then OutList is obtained from InList by sorting
% its elements according to their length frequency; i.e. in the default,
% where sorting is done ascendingly, lists with rare lengths are placed
% first, others with more frequent lengths come later.
transf(L-X,Xs,Ys,Z) :- sorry.
% Ys is the list that remains from the list Xs
% when all leading copies of length L are removed and transfed to Z
%! \end{hint}
%! \begin{solution}
% Example:
% ?- lfsort([[a,b,c],[d,e],[f,g,h],[d,e],[i,j,k,l],[m,n],[o]],L).
% L = [[i, j, k, l], [o], [a, b, c], [f, g, h], [d, e], [d,e], [m, n]]
lfsort(InList,OutList) :- lfsort(InList,OutList,asc).
% sorting direction Dir is either asc or desc
lfsort(InList,OutList,Dir) :-
add_key(InList,KList,desc),
keysort(KList,SKList),
pack(SKList,PKList),
lsort(PKList,SPKList,Dir),
flatten(SPKList,FKList),
rem_key(FKList,OutList).
pack([],[]).
pack([L-X|Xs],[[L-X|Z]|Zs]) :- transf(L-X,Xs,Ys,Z), pack(Ys,Zs).
transf(_,[],[],[]).
transf(L-_,[K-Y|Ys],[K-Y|Ys],[]) :- L \= K.
transf(L-_,[L-X|Xs],Ys,[L-X|Zs]) :- transf(L-X,Xs,Ys,Zs).
%! \end{solution} ?- lfsort([[a,b,c],[d,e],[f,g,h],[d,e],[i,j,k,l],[m,n],[o]],L).
Note that in the above example, the first two lists in the result L have length 4 and 1, both lengths appear just once. The third and fourth list have length 3 which appears, there are two list of this length. And finally, the last three lists have length 2. This is the most frequent length.
Arithmetic
Is it prime?
:- module(_, _, [assertions]).
sorry :- throw(not_solved_yet).
:- test is_prime(A) : (A = 7) + (not_fails, is_det).
%! \begin{hint}
% Example:
% ?- is_prime(7).
% Yes
is_prime(P) :- sorry.
% P is a prime number
% (integer) (+)
has_factor(N,L) :- sorry.
% N has an odd factor F >= L.
% (integer, integer) (+,+)
%! \end{hint}
%! \begin{solution}
% Example:
% ?- is_prime(7).
% Yes
is_prime(2).
is_prime(3).
is_prime(P) :- integer(P), P > 3, P mod 2 =\= 0, \+ has_factor(P,3).
has_factor(N,L) :- N mod L =:= 0.
has_factor(N,L) :- L * L < N, L2 is L + 2, has_factor(N,L2).
%! \end{solution} ?- is_prime(7).
Greatest common divisor
:- module(_, _, [assertions]).
sorry :- throw(not_solved_yet).
:- test gcd(A, B, C) : (A = 36, B = 63) => (C = 9) + (not_fails, is_det).
%! \begin{hint}
% Example:
% ?- gcd(36, 63, G).
% G = 9
gcd(X,Y,G) :- sorry.
% G is the greatest common divisor of X and Y
% (integer, integer, integer) (+,+,?)
%! \end{hint}
%! \begin{solution}
% Example:
% ?- gcd(36, 63, G).
% G = 9
gcd(X,0,X) :- X > 0.
gcd(X,Y,G) :- Y > 0, Z is X mod Y, gcd(Y,Z,G).
%! \end{solution} ?- gcd(36, 63, G).
Coprimes
:- module(_, _, [assertions]).
sorry :- throw(not_solved_yet).
:- test coprime(A, B) : (A = 35, B = 64) + (not_fails, is_det).
gcd(X,0,X) :- X > 0.
gcd(X,Y,G) :- Y > 0, Z is X mod Y, gcd(Y,Z,G).
%! \begin{hint}
% Example:
% ?- coprime(35, 64).
% yes
coprime(X,Y) :- sorry.
% X and Y are coprime.
% (integer, integer) (+,+)
%! \end{hint}
%! \begin{solution}
% Example:
% ?- coprime(35, 64).
% yes
coprime(X,Y) :- gcd(X,Y,1).
%! \end{solution} ?- coprime(35, 64).
Euler's totient function
:- module(_, _, [assertions]).
:- push_prolog_flag(multi_arity_warnings, off).
sorry :- throw(not_solved_yet).
:- test totient_phi(A, B) : (A = 10) => (B = 4) + (not_fails, is_det).
gcd(X,0,X) :- X > 0.
gcd(X,Y,G) :- Y > 0, Z is X mod Y, gcd(Y,Z,G).
coprime(X,Y) :- gcd(X,Y,1).
%! \begin{hint}
% Example:
% ?- Phi is totient_phi(10).
% Phi = 4
totient_phi(M,Phi) :- sorry.
% Phi is the value of the Euler's totient function
% phi for the argument M.
% (integer, integer) (+,-)
t_phi(M,Phi,K,C) :- sorry.
% Phi = C + N, where N is the number of integers R
% such that K <= R < M and R is coprime to M.
% (integer,integer,integer,integer) (+,-,+,+)
%! \end{hint}
%! \begin{solution}
% Example:
% ?- Phi is totient_phi(10).
% Phi = 4
totient_phi(1,1) :- !.
totient_phi(M,Phi) :- t_phi(M,Phi,1,0).
t_phi(M,Phi,M,Phi) :- !.
t_phi(M,Phi,K,C) :-
K < M, coprime(K,M), !,
C1 is C + 1, K1 is K + 1,
t_phi(M,Phi,K1,C1).
t_phi(M,Phi,K,C) :-
K < M, K1 is K + 1,
t_phi(M,Phi,K1,C).
%! \end{solution} ?- Phi is totient_phi(10)
Prime factors
:- module(_, _, [assertions]).
:- push_prolog_flag(multi_arity_warnings, off).
sorry :- throw(not_solved_yet).
:- test prime_factors(A, B) : (A = 315) => (B = [3,3,5,7]) + (not_fails, is_det).
:- test prime_factors(A, _B) : (A = 0) + (fails).
%! \begin{hint}
% Example:
% ?- prime_factors(315, L).
% L = [3,3,5,7]
prime_factors(N, L) :- sorry.
% N is the list of prime factors of N.
% (integer,list) (+,?)
prime_factors(N,L,K) :- sorry.
% L is the list of prime factors of N. It is
% known that N does not have any prime factors less than K.
next_factor(N,F,NF) :- sorry.
% when calculating the prime factors of N
% and if F does not divide N then NF is the next larger candidate to
% be a factor of N.
%! \end{hint}
%! \begin{solution}
% Example:
% ?- prime_factors(315, L).
% L = [3,3,5,7]
prime_factors(N,L) :- N > 0, prime_factors(N,L,2).
prime_factors(1,[],_) :- !.
prime_factors(N,[F|L],F) :- % N is multiple of F
R is N // F, N =:= R * F, !, prime_factors(R,L,F).
prime_factors(N,L,F) :-
next_factor(N,F,NF), prime_factors(N,L,NF). % N is not multiple of F
next_factor(_,2,3) :- !.
next_factor(N,F,NF) :- F * F < N, !, NF is F + 2.
next_factor(N,_,N). % F > sqrt(N)
%! \end{solution} ?- prime_factors(315, L).
:- module(_, _, [assertions]).
:- push_prolog_flag(multi_arity_warnings, off).
sorry :- throw(not_solved_yet).
:- test prime_factors_mult(A, B) : (A = 315) => (B = [[3,2],[5,1],[7,1]]) + (not_fails, is_det).
next_factor(_,2,3) :- !.
next_factor(N,F,NF) :- F * F < N, !, NF is F + 2.
next_factor(N,_,N). % F > sqrt(N)
%! \begin{hint}
% Example:
% ?- prime_factors_mult(315, L).
% L = [[3,2],[5,1],[7,1]]
prime_factors_mult(N, L) :- sorry.
% L is the list of prime factors of N. It is
% composed of terms [F,M] where F is a prime factor and M its multiplicity.
% (integer,list) (+,?)
prime_factors_mult(N,L,K) :- sorry.
% L is the list of prime factors of N. It is
% known that N does not have any prime factors less than K.
divide(N,F,M,R) :- sorry.
% N = R * F**M, M >= 1, and F is not a factor of R.
% (integer,integer,integer,integer) (+,+,-,-)
%! \end{hint}
%! \begin{solution}
% Example:
% ?- prime_factors_mult(315, L).
% L = [[3,2],[5,1],[7,1]]
prime_factors_mult(N,L) :- N > 0, prime_factors_mult(N,L,2).
prime_factors_mult(1,[],_) :- !.
prime_factors_mult(N,[[F,M]|L],F) :- divide(N,F,M,R), !, % F divides N
next_factor(R,F,NF), prime_factors_mult(R,L,NF).
prime_factors_mult(N,L,F) :- !, % F does not divide N
next_factor(N,F,NF), prime_factors_mult(N,L,NF).
divide(N,F,M,R) :- divi(N,F,M,R,0), M > 0.
divi(N,F,M,R,K) :- S is N // F, N =:= S * F, !, % F divides N
K1 is K + 1, divi(S,F,M,R,K1).
divi(N,_,M,N,M).
%! \end{solution} ?- prime_factors_mult(315, L).
Euler's totient function (improved)
% ?- prime_factors_mult(315, L). % L = [[3,2],[5,1],[7,1]]then the function can be efficiently calculated as follows: Let [[p1,m1],[p2,m2],[p3,m3],...] be the list of prime factors (and their multiplicities) of a given number m. Then phi(m) can be calculated with the following formula: Note that stands for the 'th power of .
:- module(_, _, [assertions]).
:- push_prolog_flag(multi_arity_warnings, off).
sorry :- throw(not_solved_yet).
prime_factors_mult(N,L) :- N > 0, prime_factors_mult(N,L,2).
prime_factors_mult(1,[],_) :- !.
prime_factors_mult(N,[[F,M]|L],F) :- divide(N,F,M,R), !, % F divides N
next_factor(R,F,NF), prime_factors_mult(R,L,NF).
prime_factors_mult(N,L,F) :- !, % F does not divide N
next_factor(N,F,NF), prime_factors_mult(N,L,NF).
divide(N,F,M,R) :- divi(N,F,M,R,0), M > 0.
divi(N,F,M,R,K) :- S is N // F, N =:= S * F, !, % F divides N
K1 is K + 1, divi(S,F,M,R,K1).
divi(N,_,M,N,M).
next_factor(_,2,3) :- !.
next_factor(N,F,NF) :- F * F < N, !, NF is F + 2.
next_factor(N,_,N). % F > sqrt(N)
:- test totient_phi_2(A,B) : (A = 315) => (B = 144) + (not_fails, is_det).
%! \begin{hint}
% Example:
% ?- totient_phi_2(315, N).
% N = 144
totient_phi_2(N,Phi) :- sorry.
% Phi is the value of Euler's totient function
% for the argument N.
% (integer,integer) (+,?)
%! \end{hint}
%! \begin{solution}
% Example:
% ?- totient_phi_2(315, N).
% N = 144
totient_phi_2(N,Phi) :- prime_factors_mult(N,L), to_phi(L,Phi).
to_phi([],1).
to_phi([[F,1]|L],Phi) :- !,
to_phi(L,Phi1), Phi is Phi1 * (F - 1).
to_phi([[F,M]|L],Phi) :- M > 1,
M1 is M - 1, to_phi([[F,M1]|L],Phi1), Phi is Phi1 * F.
%! \end{solution} ?- totient_phi_2(315, N).
Comparing Euler's totient function's methods
List of prime numbers
:- module(_, _, [assertions]).
sorry :- throw(not_solved_yet).
is_prime(2).
is_prime(3).
is_prime(P) :- integer(P), P > 3, P mod 2 =\= 0, \+ has_factor(P,3).
has_factor(N,L) :- N mod L =:= 0.
has_factor(N,L) :- L * L < N, L2 is L + 2, has_factor(N,L2).
:- test prime_list(A,B,C) : (A = 1, B = 50)
=> (C = [2,3,5,7,11,13,17,19,23,29,31,37,41,43,47]) + (not_fails, is_det).
%! \begin{hint}
% Example:
% ?- prime_list(1,10,L).
% [2,3,5,7]
prime_list(A,B,L) :- sorry.
% L is the list of prime number P with A <= P <= B
%! \end{hint}
%! \begin{solution}
% Example:
% ?- prime_list(1,10,L).
% [2,3,5,7]
prime_list(A,B,L) :- A =< 2, !, p_list(2,B,L).
prime_list(A,B,L) :- A1 is (A // 2) * 2 + 1, p_list(A1,B,L).
p_list(A,B,[]) :- A > B, !.
p_list(A,B,[A|L]) :- is_prime(A), !,
next(A,A1), p_list(A1,B,L).
p_list(A,B,L) :-
next(A,A1), p_list(A1,B,L).
next(2,3) :- !.
next(A,A1) :- A1 is A + 2.
%! \end{solution} ?- prime_list(1,10,L).
Goldbach's conjecture
:- module(_, _, [assertions]).
:- push_prolog_flag(multi_arity_warnings, off).
sorry :- throw(not_solved_yet).
is_prime(2).
is_prime(3).
is_prime(P) :- integer(P), P > 3, P mod 2 =\= 0, \+ has_factor(P,3).
has_factor(N,L) :- N mod L =:= 0.
has_factor(N,L) :- L * L < N, L2 is L + 2, has_factor(N,L2).
:- test goldbach(A,B) : (A = 28) => (B = [5,23]) + (not_fails, is_det).
:- test goldbach(A,B) : (A = 4) => (B = [2,2]) + (not_fails, is_det).
%! \begin{hint}
% Example:
% ?- goldbach(28, L).
% L = [5,23]
goldbach(N,L) :- sorry.
% L is the list of the two prime numbers that
% sum up to the given N (which must be even).
% (integer,integer) (+,-)
%! \end{hint}
%! \begin{solution}
% Example:
% ?- goldbach(28, L).
% L = [5,23]
goldbach(4,[2,2]) :- !.
goldbach(N,L) :- N mod 2 =:= 0, N > 4, goldbach(N,L,3).
goldbach(N,[P,Q],P) :- Q is N - P, is_prime(Q), !.
goldbach(N,L,P) :- P < N, next_prime(P,P1), goldbach(N,L,P1).
next_prime(P,P1) :- P1 is P + 2, is_prime(P1), !.
next_prime(P,P1) :- P2 is P + 2, next_prime(P2,P1).
%! \end{solution} ?- goldbach(28, L).
List of Goldbach compositions
In most cases, if an even number is written as the sum of two prime numbers, one of them is very small. Very rarely, the primes are both bigger than say 50. Try to find out how many such cases there are in the range 2..3000. Example (for a print limit of 50): ?- goldbach_list(1,2000,50). ; ; ;
:- module(_, _, [assertions]).
:- use_module(library(streams), [nl/0, display/1]).
:- push_prolog_flag(multi_arity_warnings, off).
sorry :- throw(not_solved_yet).
is_prime(2).
is_prime(3).
is_prime(P) :- integer(P), P > 3, P mod 2 =\= 0, \+ has_factor(P,3).
has_factor(N,L) :- N mod L =:= 0.
has_factor(N,L) :- L * L < N, L2 is L + 2, has_factor(N,L2).
goldbach(4,[2,2]) :- !.
goldbach(N,L) :- N mod 2 =:= 0, N > 4, goldbach(N,L,3).
goldbach(N,[P,Q],P) :- Q is N - P, is_prime(Q), !.
goldbach(N,L,P) :- P < N, next_prime(P,P1), goldbach(N,L,P1).
next_prime(P,P1) :- P1 is P + 2, is_prime(P1), !.
next_prime(P,P1) :- P2 is P + 2, next_prime(P2,P1).
%! \begin{hint}
goldbach_list(A,B) :- sorry.
% print a list of the Goldbach composition
% of all even numbers N in the range A <= N <= B
% (integer,integer) (+,+)
goldbach_list(A,B,L) :- sorry.
% perform goldbach_list(A,B), but suppress
% all output when the first prime number is less than the limit L.
%! \end{hint}
%! \begin{solution}
goldbach_list(A,B) :- goldbach_list(A,B,2).
goldbach_list(A,B,L) :- A =< 4, !, g_list(4,B,L).
goldbach_list(A,B,L) :- A1 is ((A+1) // 2) * 2, g_list(A1,B,L).
g_list(A,B,_) :- A > B, !.
g_list(A,B,L) :-
goldbach(A,[P,Q]),
print_goldbach(A,P,Q,L),
A2 is A + 2,
g_list(A2,B,L).
print_goldbach(A,P,Q,L) :- P >= L, !,
display(A),
display(' = '),
display(P),
display(' + '),
display(Q), nl.
print_goldbach(_,_,_,_).
%! \end{solution} Load your code and check if the answer to the query ?- goldbach_list(9, 20) is the same as state above. If not try again! ?- goldbach_list(9, 20).
Logic and Codes
Truth tables
:- module(_, _, [assertions]).
:- use_module(library(streams), [nl/0, display/1]).
:- use_module(engine(hiord_rt), [call/1]).
sorry :- throw(not_solved_yet).
%! \begin{hint}
% Example:
% ?- table(A,B,and(A,or(A,B))).
% true true true
% true fail true
% fail true fail
% fail fail fail
table(A,B,Expr) :- sorry.
%! \end{hint}
%! \begin{solution}
% Example:
% ?- table(A,B,and(A,or(A,B))).
% true true true
% true fail true
% fail true fail
% fail fail fail
not(true) :-
false.
not(false) :-
true.
and(A,B) :- A, B.
or(A,_) :- A.
or(_,B) :- B.
equ(A,B) :- or(and(A,B), and(not(A),not(B))).
xor(A,B) :- not(equ(A,B)).
nor(A,B) :- not(or(A,B)).
nand(A,B) :- not(and(A,B)).
impl(A,B) :- or(not(A),B).
% bind(X) :- instantiate X to be true and false successively
bind(true).
bind(fail).
table(A,B,Expr) :- bind(A), bind(B), do(A,B,Expr), fail.
do(A,B,_) :- display(A), display(' '), display(B), display(' '), fail.
do(_,_,Expr) :- Expr, !, display('true'), nl.
do(_,_,_) :- display('fail'), nl.
%! \end{solution} Load your code and check if the answer to the query ?- table(A,B,and(A,or(A,B))) is: true true true true fail true fail true fail fail fail failIf not, try again!
?- table(A,B,and(A,or(A,B))).
Gray code
:- module(_, _, [assertions, dynamic]).
:- use_module(library(classic/classic_predicates),[reverse/2, append/3]).
sorry :- throw(not_solved_yet).
:- test gray_c(A,B) : (A = 5) =>(B = ['00000','00001','00011','00010','00110','00111','00101','00100','01100','01101','01111','01110','01010','01011','01001','01000','11000','11001','11011','11010','11110','11111','11101','11100','10100','10101','10111','10110','10010','10011','10001','10000']) + (not_fails, is_det).
%! \begin{hint}
% Find out the construction rules and write a predicate with the
% following specification:
gray(N,C) :- sorry.
% C is the N-bit Gray code
% Can you apply the method of "result caching" in order to make the
% predicate more efficient, when it is to be used repeatedly?
%! \end{hint}
%! \begin{solution}
gray(1,['0','1']).
gray(N,C) :- N > 1, N1 is N-1,
gray(N1,C1), reverse(C1,C2),
prepend('0',C1,C1P),
prepend('1',C2,C2P),
append(C1P,C2P,C).
prepend(_,[],[]) :- !.
prepend(X,[C|Cs],[CP|CPs]) :- atom_concat(X,C,CP), prepend(X,Cs,CPs).
% This gives a nice example for the result caching technique:
:- dynamic gray_c/2.
gray_c(1,['0','1']) :- !.
gray_c(N,C) :- N > 1, N1 is N-1,
gray_c(N1,C1), reverse(C1,C2),
prepend('0',C1,C1P),
prepend('1',C2,C2P),
append(C1P,C2P,C),
asserta((gray_c(N,C) :- !)).
%! \end{solution} ?- gray_c(5,C).
Huffman code
:- module(_, _, [assertions]).
:- use_module(library(terms), [atom_concat/2]).
:- use_module(library(sort)).
:- push_prolog_flag(multi_arity_warnings, off).
:- test huffman(A,B) : (A =[fr(a,45),fr(b,13),fr(c,12),fr(d,16),fr(e,9),fr(f,5)])
=> (B = [hc(a,'0'),hc(b,'101'),hc(c,'100'),hc(d,'111'),hc(e,'1101'),hc(f,'1100')]) + (not_fails, is_det).
sorry :- throw(not_solved_yet).
%! \begin{hint}
% Example
% ?- huffman([fr(a,45),fr(b,13),fr(c,12),fr(d,16),fr(e,9),fr(f,5)],C).
% C = [hc(a,'0'),hc(b,'101'),hc(c,'100'),hc(d,'111'),hc(e,'1101'),hc(f,'1100')]
huffman(Fs,Hs) :- sorry.
% Hs is the Huffman code table for the frequency table Fs
% (list-of-fr/2-terms, list-of-hc/2-terms) (+,-).
%! \end{hint}
%! \begin{solution}
% Example
% ?- huffman([fr(a,45),fr(b,13),fr(c,12),fr(d,16),fr(e,9),fr(f,5)],C).
% C = [hc(a,'0'),hc(b,'101'),hc(c,'100'),hc(d,'111'),hc(e,'1101'),hc(f,'1100')]+
% During the construction process, we need nodes n(F,S) where, at the
% beginning, F is a frequency and S a symbol. During the process, as n(F,S)
% becomes an internal node, S becomes a term s(L,R) with L and R being
% again n(F,S) terms. A list of n(F,S) terms, called Ns, is maintained
% as a sort of priority queue.
huffman(Fs,Cs) :-
initialize(Fs,Ns),
make_tree(Ns,T),
traverse_tree(T,Cs).
initialize(Fs,Ns) :- init(Fs,NsU), sort(NsU,Ns).
init([],[]).
init([fr(S,F)|Fs],[n(F,S)|Ns]) :- init(Fs,Ns).
make_tree([T],T).
make_tree([n(F1,X1),n(F2,X2)|Ns],T) :-
F is F1+F2,
insert(n(F,s(n(F1,X1),n(F2,X2))),Ns,NsR),
make_tree(NsR,T).
% insert(n(F,X),Ns,NsR) :- insert the node n(F,X) into Ns such that the
% resulting list NsR is again sorted with respect to the frequency F.
insert(N,[],[N]) :- !.
insert(n(F,X),[n(F0,Y)|Ns],[n(F,X),n(F0,Y)|Ns]) :- F < F0, !.
insert(n(F,X),[n(F0,Y)|Ns],[n(F0,Y)|Ns1]) :- F >= F0, insert(n(F,X),Ns,Ns1).
% traverse_tree(T,Cs) :- traverse the tree T and construct the Huffman
% code table Cs,
traverse_tree(T,Cs) :- traverse_tree(T,'',Cs1-[]), sort(Cs1,Cs).
traverse_tree(n(_,A),Code,[hc(A,Code)|Cs]-Cs) :- atom(A). % leaf node
traverse_tree(n(_,s(Left,Right)),Code,Cs1-Cs3) :- % internal node
atom_concat(Code,'0',CodeLeft),
atom_concat(Code,'1',CodeRight),
traverse_tree(Left,CodeLeft,Cs1-Cs2),
traverse_tree(Right,CodeRight,Cs2-Cs3).
%! \end{solution} ?- huffman([fr(a,45),fr(b,13),fr(c,12),fr(d,16),fr(e,9),fr(f,5)],C).
Binary Trees
A binary tree is either empty or it is composed of a root element and two successors, which are binary trees themselves.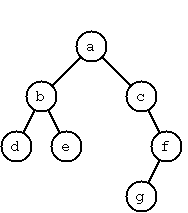
In Prolog we represent the empty tree by the atom 'nil' and the non-empty tree by the term t(X,L,R), where X denotes the root node and L and R denote the left and right subtree, respectively.
The example tree depicted opposite is therefore represented by the following Prolog term:
T1 = t(a,t(b,t(d,nil,nil),t(e,nil,nil)),t(c,nil,t(f,t(g,nil,nil),nil))).
Other examples are a binary tree that consists of a root node only: T2 = t(a,nil,nil) or an empty binary tree: T3 = nil. You can check your predicates using these example trees. They are given as test cases in Is it a binary tree? problem.
Is it a binary tree?
:- module(_, _, [assertions]).
:- test istree(A) : (A = (t(a,t(b,t(d,nil,nil),t(e,nil,nil)),t(c,nil,t(f,t(g,nil,nil),nil))))) + (not_fails, is_det).
:- test istree(A) : (A = nil) + (not_fails, is_det).
:- test istree(A) : (A = (t(a,nil,nil))) + (not_fails, is_det).
sorry :- throw(not_solved_yet).
%! \begin{hint}
% Example
% ?- istree(t(a,t(b,nil,nil))).
% No
istree(T) :- sorry.
% T is a term representing a binary tree (i), (o)
%! \end{hint}
%! \begin{solution}
% Example
% ?- istree(t(a,t(b,nil,nil))).
% No
istree(nil).
istree(t(_,L,R)) :- istree(L), istree(R).
%! \end{solution}?- istree(t(a,t(b,nil,nil),nil)).
Balanced binary trees
:- module(_, _, [assertions]).
sorry :- throw(not_solved_yet).
:- test cbal_tree(A,T) : (A = 1) => (T = t(x,nil,nil)) + (not_fails, is_det) .
%! \begin{hint}
% Example
% ?- cbal_tree(4,T).
% T = t(x, t(x, nil, nil), t(x, nil, t(x, nil, nil))) ;
% T = t(x, t(x, nil, nil), t(x, t(x, nil, nil), nil)) ;
% etc.
cbal_tree(N,T) :- sorry.
% T is a completely balanced binary tree with N nodes.
% (integer, tree) (+,?)
%! \end{hint}
%! \begin{solution}
% Example
% ?- cbal_tree(4,T).
% T = t(x, t(x, nil, nil), t(x, nil, t(x, nil, nil))) ;
% T = t(x, t(x, nil, nil), t(x, t(x, nil, nil), nil)) ;
% etc.
cbal_tree(0,nil) :- !.
cbal_tree(N,t(x,L,R)) :- N > 0,
N0 is N - 1,
N1 is N0//2, N2 is N0 - N1,
distrib(N1,N2,NL,NR),
cbal_tree(NL,L), cbal_tree(NR,R).
distrib(N,N,N,N) :- !.
distrib(N1,N2,N1,N2).
distrib(N1,N2,N2,N1).
%! \end{solution}?- cbal_tree(4,T).
Symmetric binary trees
:- module(_, _, [assertions]).
sorry :- throw(not_solved_yet).
:- test symmetric(A) : (A = nil) + (not_fails, is_det) .
:- test symmetric(A) : (A = t(5,t(3,t(1,nil,nil),t(4,nil,nil)),t(18,t(12,nil,nil),t(21,nil,nil)))) + (not_fails, is_det).
%! \begin{hint}
% Example
% ?- symmetric(t(5,t(3,t(1,nil,nil),t(4,nil,nil)),t(18,t(12,nil,nil),t(21,nil,nil))))
% yes
symmetric(T) :- sorry.
% the binary tree T is symmetric.
%! \end{hint}
%! \begin{solution}
% Example
% ?- symmetric(t(5,t(3,t(1,nil,nil),t(4,nil,nil)),t(18,t(12,nil,nil),t(21,nil,nil))))
% yes
symmetric(nil).
symmetric(t(_,L,R)) :- mirror(L,R).
mirror(nil,nil).
mirror(t(_,L1,R1),t(_,L2,R2)) :- mirror(L1,R2), mirror(R1,L2).
%! \end{solution}?- symmetric(t(5,t(3,t(1,nil,nil),t(4,nil,nil)),t(18,t(12,nil,nil),t(21,nil,nil))))
Binary search trees (dictionaries)
:- module(_, _, [assertions]).
:- push_prolog_flag(multi_arity_warnings, off).
sorry :- throw(not_solved_yet).
:- test construct(A,B) : (A = []) => (B = nil) + (not_fails, is_det).
:- test construct(A,B) : (A = [3,2,5,7,1]) => (B = t(3, t(2, t(1, nil, nil), nil), t(5, nil, t(7, nil, nil)))) + (not_fails, is_det).
%! \begin{hint}
% Example
% ?- construct([3,2,5,7,1],T).
% T = t(3, t(2, t(1, nil, nil), nil), t(5, nil, t(7, nil, nil)))
construct(L,T) :- sorry.
add(X,T1,T2) :- sorry.
% the binary dictionary T2 is obtained by
% adding the item X to the binary dictionary T1
% (element,binary-dictionary,binary-dictionary) (i,i,o)
%! \end{hint}
%! \begin{solution}
% Example
% ?- construct([3,2,5,7,1],T).
% T = t(3, t(2, t(1, nil, nil), nil), t(5, nil, t(7, nil, nil)))
add(X,nil,t(X,nil,nil)).
add(X,t(Root,L,R),t(Root,L1,R)) :- X @< Root, add(X,L,L1).
add(X,t(Root,L,R),t(Root,L,R1)) :- X @> Root, add(X,R,R1).
construct(L,T) :- construct(L,T,nil).
construct([],T,T).
construct([N|Ns],T,T0) :- add(N,T0,T1), construct(Ns,T,T1).
%! \end{solution}?- construct([3,2,5,7,1],T).
Generate-and-test paradigm
:- module(_, _, [assertions]).
:- use_module(library(streams), [nl/0, display/1]).
:- use_module(library(aggregates), [setof/3]).
:- use_module(library(classic/classic_predicates), [between/3, length/2]).
sorry :- throw(not_solved_yet).
:- test sym_cbal_trees(A,Ts) : (A = 5) => (Ts = [t(x, t(x, nil, t(x, nil, nil)), t(x, t(x, nil, nil), nil)),t(x, t(x, t(x, nil, nil), nil), t(x, nil, t(x, nil, nil)))]) + (not_fails, is_det).
symmetric(nil).
symmetric(t(_,L,R)) :- mirror(L,R).
mirror(nil,nil).
mirror(t(_,L1,R1),t(_,L2,R2)) :- mirror(L1,R2), mirror(R1,L2).
cbal_tree(0,nil) :- !.
cbal_tree(N,t(x,L,R)) :- N > 0,
N0 is N - 1,
N1 is N0//2, N2 is N0 - N1,
distrib(N1,N2,NL,NR),
cbal_tree(NL,L), cbal_tree(NR,R).
distrib(N,N,N,N) :- !.
distrib(N1,N2,N1,N2).
distrib(N1,N2,N2,N1).
%! \begin{hint}
% Example
% ?- sym_cbal_trees(5,Ts).
% Ts = [t(x, t(x, nil, t(x, nil, nil)), t(x, t(x, nil, nil), nil)),
% t(x, t(x, t(x, nil, nil), nil), t(x, nil, t(x, nil, nil)))]
sym_cbal_tree(N,T) :- sorry.
%! \end{hint}
%! \begin{solution}
% Example
% ?- sym_cbal_trees(5,Ts).
% Ts = [t(x, t(x, nil, t(x, nil, nil)), t(x, t(x, nil, nil), nil)),
% t(x, t(x, t(x, nil, nil), nil), t(x, nil, t(x, nil, nil)))]
sym_cbal_tree(N,T) :- cbal_tree(N,T), symmetric(T).
sym_cbal_trees(N,Ts) :- setof(T,sym_cbal_tree(N,T),Ts).
investigate(A,B) :-
between(A,B,N),
sym_cbal_trees(N,Ts), length(Ts,L),
display(N), display(' '), display(L), nl,
fail.
investigate(_,_).
%! \end{solution}?- sym_cbal_trees(5,Ts).How many such trees are there with 57 nodes? How many solutions there are for a given number of nodes? What if the number is even? Write an appropriate predicate.
Height-balanced binary trees
:- module(_, _, [assertions]).
sorry :- throw(not_solved_yet).
:- test hbal_tree(A,T) : (A = 0) => (T = nil) + (not_fails, is_det).
:- test hbal_tree(A,T) : (A = 1) => (T = t(x,nil,nil)) + (not_fails, is_det).
%! \begin{hint}
% Example
% ?- hbal_tree(3,T).
% T = t(x, t(x, t(x, nil, nil), t(x, nil, nil)), t(x, t(x, nil, nil),t(x, nil, nil))) ;
% T = t(x, t(x, t(x, nil, nil), t(x, nil, nil)), t(x, t(x, nil, nil),nil)) ;
% etc.
hbal_tree(D,T) :- sorry.
% T is a height-balanced binary tree with depth T
%! \end{hint}
%! \begin{solution}
% Example
% ?- hbal_tree(3,T).
% T = t(x, t(x, t(x, nil, nil), t(x, nil, nil)), t(x, t(x, nil, nil),t(x, nil, nil))) ;
% T = t(x, t(x, t(x, nil, nil), t(x, nil, nil)), t(x, t(x, nil, nil),nil)) ;
% etc.
hbal_tree(0,nil) :- !.
hbal_tree(1,t(x,nil,nil)) :- !.
hbal_tree(D,t(x,L,R)) :- D > 1,
D1 is D - 1, D2 is D - 2,
distr(D1,D2,DL,DR),
hbal_tree(DL,L), hbal_tree(DR,R).
distr(D1,_,D1,D1).
distr(D1,D2,D1,D2).
distr(D1,D2,D2,D1).
%! \end{solution}?- hbal_tree(3,T).
:- module(_, _, [assertions]).
:- use_module(library(aggregates), [setof/3]).
:- use_module(library(classic/classic_predicates), [between/3, length/2]).
:- push_prolog_flag(multi_arity_warnings, off).
sorry :- throw(not_solved_yet).
:- test hbal_tree_nodes(A,T) : (A = 0) => (T = nil) + (not_fails, is_det).
:- test hbal_tree_nodes(A,T) : (A = 1) => (T = t(x,nil,nil)) + (not_fails, is_det).
:- test hbal_tree_nodes(A,T) : (A = 3) => (T = t(x,t(x,nil,nil),t(x,nil,nil))) + (not_fails, is_det).
hbal_tree(0,nil) :- !.
hbal_tree(1,t(x,nil,nil)) :- !.
hbal_tree(D,t(x,L,R)) :- D > 1,
D1 is D - 1, D2 is D - 2,
distr(D1,D2,DL,DR),
hbal_tree(DL,L), hbal_tree(DR,R).
distr(D1,_,D1,D1).
distr(D1,D2,D1,D2).
distr(D1,D2,D2,D1).
%! \begin{hint}
% Example
% ?- hbal_tree_nodes(3,T).
% T = t(x,t(x,nil,nil),t(x,nil,nil))
minNodes(H,N) :- sorry.
% N is the minimum number of nodes in a height-balanced binary tree of height H
% (integer,integer) (+,?)
maxNodes(H,N) :- sorry.
% N is the maximum number of nodes in a height-balanced binary tree of height H
% (integer,integer) (+,?)
minHeight(N,H) :- sorry.
% H is the minimum height of a height-balanced binary tree with N nodes
% (integer,integer) (+,?)
maxHeight(N,H) :- sorry.
% H is the maximum height of a height-balanced binary tree with N nodes
% (integer,integer), (+,?)
% Now, we can attack the main problem: construct all the
% height-balanced binary trees with a given number of nodes.
hbal_tree_nodes(N,T) :- sorry.
% T is a height-balanced binary tree with N nodes.
% T is a height-balanced binary tree with N nodes.
%! \end{hint}
%! \begin{solution}
% Example
% ?- hbal_tree_nodes(3,T).
% T = t(x,t(x,nil,nil),t(x,nil,nil))
minNodes(0,0) :- !.
minNodes(1,1) :- !.
minNodes(H,N) :- H > 1,
H1 is H - 1, H2 is H - 2,
minNodes(H1,N1), minNodes(H2,N2),
N is 1 + N1 + N2.
maxNodes(H,N) :- N is 2**H - 1.
minHeight(0,0) :- !.
minHeight(N,H) :- N > 0, N1 is N//2, minHeight(N1,H1), H is H1 + 1.
maxHeight(N,H) :- maxHeight(N,H,1,1).
maxHeight(N,H,H1,N1) :- N1 > N, !, H is H1 - 1.
maxHeight(N,H,H1,N1) :- N1 =< N,
H2 is H1 + 1, minNodes(H2,N2), maxHeight(N,H,H2,N2).
hbal_tree_nodes(N,T) :-
minHeight(N,Hmin), maxHeight(N,Hmax),
between(Hmin,Hmax,H),
hbal_tree(H,T), nodes(T,N).
% nodes(T,N) :- the binary tree T has N nodes
% (tree,integer); (i,*)
nodes(nil,0).
nodes(t(_,Left,Right),N) :-
nodes(Left,NLeft),
nodes(Right,NRight),
N is NLeft + NRight + 1.
count_hbal_trees(N,C) :- setof(T,hbal_tree_nodes(N,T),Ts), length(Ts,C).
%! \end{solution}Find out how many height-balanced trees exist for N = 15. ?- count_hbal_trees(15,C).
Leaves of a binary tree
:- module(_, _, [assertions]).
:- test count_leaves(A,B) : (A = nil) => (B = 0) + (not_fails, is_det).
:- test count_leaves(A,B) : (A = t(_,nil,nil)) => (B = 1) + (not_fails, is_det).
:- test count_leaves(A,B) : (A = t(x, t(x, t(x, nil, nil), t(x, nil, nil)), t(x, t(x, nil, nil),t(x, nil, nil)))) => (B = 4) + (not_fails, is_det).
sorry :- throw(not_solved_yet).
%! \begin{hint}
% Example
% ?- count_leaves(t(x, t(x, t(x, nil, nil), t(x, nil, nil)), t(x, t(x, nil, nil),t(x, nil, nil))),B).
% B = 4
count_leaves(T,N) :- sorry.
% the binary tree T has N leaves
%! \end{hint}
%! \begin{solution}
% Example
% ?- count_leaves(t(x, t(x, t(x, nil, nil), t(x, nil, nil)), t(x, t(x, nil, nil),t(x, nil, nil))),B).
% B = 4
count_leaves(nil,0).
count_leaves(t(_,nil,nil),1).
count_leaves(t(_,L,nil),N) :- L = t(_,_,_), count_leaves(L,N).
count_leaves(t(_,nil,R),N) :- R = t(_,_,_), count_leaves(R,N).
count_leaves(t(_,L,R),N) :- L = t(_,_,_), R = t(_,_,_),
count_leaves(L,NL), count_leaves(R,NR), N is NL + NR.
% The above solution works in the flow patterns (i,o) and (i,i)
% without cut and produces a single correct result. Using a cut
% we can obtain the same result in a much shorter program, like this:
count_leaves1(nil,0).
count_leaves1(t(_,nil,nil),1) :- !.
count_leaves1(t(_,L,R),N) :-
count_leaves1(L,NL), count_leaves1(R,NR), N is NL+NR.
% For the flow pattern (o,i) see P61A
%! \end{solution}?- count_leaves(t(x, t(x, t(x, nil, nil), t(x, nil, nil)), t(x, t(x, nil, nil),t(x, nil, nil))),B).
:- module(_, _, [assertions]).
:- use_module(library(classic/classic_predicates), [between/3, append/3]).
:- push_prolog_flag(multi_arity_warnings, off).
:- test leaves(A,B) : (A = nil) => (B = []) + (not_fails, is_det).
:- test leaves(A,B) : (A = t(x,nil,nil)) => (B = [x]) + (not_fails, is_det).
:- test leaves(A,B) : (A = t(x, t(x, t(x, nil, nil), t(x, nil, nil)), t(x, t(x, nil, nil),t(x, nil, nil)))) => (B = [x,x,x,x]) + (not_fails, is_det).
sorry :- throw(not_solved_yet).
%! \begin{hint}
% Example
% ?- count_leaves(t(x, t(x, t(x, nil, nil), t(x, nil, nil)), t(x, t(x, nil, nil),t(x, nil, nil))),B).
% B = [x,x,x,x]
leaves(T,S) :- sorry.
% S is the list of the leaves of the binary tree T
nnodes(T,N) :- sorry.
% T is a binary tree with N nodes (o,i)
leaves2(T,S) :- sorry.
% S is the list of leaves of the tree T (o,i)
%! \end{hint}
%! \begin{solution}
% Example
% ?- count_leaves(t(x, t(x, t(x, nil, nil), t(x, nil, nil)), t(x, t(x, nil, nil),t(x, nil, nil))),B).
% B = [x,x,x,x]
leaves(nil,[]).
leaves(t(X,nil,nil),[X]).
leaves(t(_,L,nil),S) :- L = t(_,_,_), leaves(L,S).
leaves(t(_,nil,R),S) :- R = t(_,_,_), leaves(R,S).
leaves(t(_,L,R),S) :- L = t(_,_,_), R = t(_,_,_),
leaves(L,SL), leaves(R,SR), append(SL,SR,S).
% The above solution works in the flow patterns (i,o) and (i,i)
% without cut and produces a single correct result. Using a cut
% we can obtain the same result in a much shorter program, like this:
leaves1(nil,[]).
leaves1(t(X,nil,nil),[X]) :- !.
leaves1(t(_,L,R),S) :-
leaves1(L,SL), leaves1(R,SR), append(SL,SR,S).
% To write a predicate that works in the flow pattern (o,i)
% is a more difficult problem, because using append/3 in
% the flow pattern (o,o,i) always generates an empty list
% as first solution and the result is an infinite recursion
% along the left subtree of the generated binary tree.
% A possible solution is the following trick: we successively
% construct binary tree structures for a given number of nodes
% and fill the leaf nodes with the elements of the leaf list.
% We then increment the number of tree nodes successively,
% and so on.
nnodes(nil,0) :- !.
nnodes(t(_,L,R),N) :- N > 0, N1 is N-1,
between(0,N1,NL), NR is N1-NL,
nnodes(L,NL), nnodes(R,NR).
leaves2(T,S) :- leaves2(T,S,0).
leaves2(T,S,N) :- nnodes(T,N), leaves1(T,S).
leaves2(T,S,N) :- N1 is N+1, leaves2(T,S,N1).
%! \end{solution}?- leaves(t(x, t(x, t(x, nil, nil), t(x, nil, nil)), t(x, t(x, nil, nil),t(x, nil, nil))),B).
Nodes of a binary tree
:- module(_, _, [assertions]).
:- use_module(library(classic/classic_predicates), [append/3]).
:- test internals(A,B) : (A = nil) => (B = []) + (not_fails, is_det).
:- test internals(A,B) : (A = t(_,nil,nil)) => (B = []) + (not_fails, is_det).
:- test internals(A,B) : (A = t(x, t(x, t(x, nil, nil), t(x, nil, nil)), t(x, t(x, nil, nil),t(x, nil, nil)))) => (B = [x,x,x]) + (not_fails, is_det).
sorry :- throw(not_solved_yet).
%! \begin{hint}
% Example
% ?- internals(t(x, t(x, t(x, nil, nil), t(x, nil, nil)), t(x, t(x, nil, nil),t(x, nil, nil))),B).
% B = [x,x,x]
internals(T,S) :- sorry.
% S is the list of internal nodes of the binary tree T.
%! \end{hint}
%! \begin{solution}
% Example
% ?- internals(t(x, t(x, t(x, nil, nil), t(x, nil, nil)), t(x, t(x, nil, nil),t(x, nil, nil))),B).
% B = [x,x,x]
internals(nil,[]).
internals(t(_,nil,nil),[]).
internals(t(X,L,nil),[X|S]) :- L = t(_,_,_), internals(L,S).
internals(t(X,nil,R),[X|S]) :- R = t(_,_,_), internals(R,S).
internals(t(X,L,R),[X|S]) :- L = t(_,_,_), R = t(_,_,_),
internals(L,SL), internals(R,SR), append(SL,SR,S).
% The above solution works in the flow patterns (i,o) and (i,i)
% without cut and produces a single correct result. Using a cut
% we can obtain the same result in a much shorter program, like this:
internals1(nil,[]).
internals1(t(_,nil,nil),[]) :- !.
internals1(t(X,L,R),[X|S]) :-
internals1(L,SL), internals1(R,SR), append(SL,SR,S).
% For the flow pattern (o,i) there is the following very
% elegant solution:
internals2(nil,[]).
internals2(t(X,L,R),[X|S]) :-
append(SL,SR,S), internals2(L,SL), internals2(R,SR).
%! \end{solution}?- internals(t(x, t(x, t(x, nil, nil), t(x, nil, nil)), t(x, t(x, nil, nil),t(x, nil, nil))),B).
:- module(_, _, [assertions]).
:- use_module(library(classic/classic_predicates), [between/3, append/3]).
:- push_prolog_flag(multi_arity_warnings, off).
:- test atlevel(A,_B,C) : (A = nil) => (C = []) + (not_fails, is_det).
:- test atlevel(A,B,C) : (A = t(X,_,_), B = 1) => (C = [X]) + (not_fails, is_det).
:- test atlevel(A,B,C) : (A = t(x, t(x, t(x, nil, nil), t(x, nil, nil)), t(x, t(x, nil, nil),t(x, nil, nil))), B = 2) => (C = [x,x]) + (not_fails, is_det).
sorry :- throw(not_solved_yet).
%! \begin{hint}
% Example
% ?- atlevel(t(x, t(x, t(x, nil, nil), t(x, nil, nil)), t(x, t(x, nil, nil),t(x, nil, nil))),2,C).
% B = [x,x]
atlevel(T,L,S) :- sorry.
% S is the list of nodes of the binary tree T at level L
%! \end{hint}
%! \begin{solution}
% Example
% ?- atlevel(t(x, t(x, t(x, nil, nil), t(x, nil, nil)), t(x, t(x, nil, nil),t(x, nil, nil))),2,C).
% B = [x,x]
atlevel(nil,_,[]).
atlevel(t(X,_,_),1,[X]).
atlevel(t(_,L,R),D,S) :- D > 1, D1 is D-1,
atlevel(L,D1,SL), atlevel(R,D1,SR), append(SL,SR,S).
% The following is a quick-and-dirty solution for the
% level-order sequence
levelorder(T,S) :- levelorder(T,S,1).
levelorder(T,[],D) :- atlevel(T,D,[]), !.
levelorder(T,S,D) :- atlevel(T,D,SD),
D1 is D+1, levelorder(T,S1,D1), append(SD,S1,S).
%! \end{solution}?- atlevel(t(x, t(x, t(x, nil, nil), t(x, nil, nil)), t(x, t(x, nil, nil),t(x, nil, nil))),2,T).
Complete binary tree
We can assign an address number to each node in a complete binary tree by enumerating the nodes in level order, starting at the root with number 1. In doing so, we realize that for every node X with address A the following property holds: The address of X's left and right successors are 2*A and 2*A+1, respectively, supposed the successors do exist. This fact can be used to elegantly construct a complete binary tree structure. Write a predicate complete_binary_tree/2.
:- module(_, _, [assertions]).
:- use_module(library(classic/classic_predicates), [length/2]).
:- push_prolog_flag(multi_arity_warnings, off).
:- test complete_binary_tree(A,B) : (A = 0) => (B = nil) + (not_fails, is_det).
:- test complete_binary_tree(A,B) : (A = 1) => (B = t(_,nil,nil)) + (not_fails, is_det).
:- test complete_binary_tree(A,B) : (A = 2) => (B = t(_,t(_,nil,nil),nil)) + (not_fails, is_det).
sorry :- throw(not_solved_yet).
%! \begin{hint}
complete_binary_tree(N,T) :- sorry.
% T is a complete binary tree with N nodes. (+,?)
%! \end{hint}
%! \begin{solution}
complete_binary_tree(N,T) :-
complete_binary_tree(N,T,1).
complete_binary_tree(N,nil,A) :- A > N, !.
complete_binary_tree(N,t(_,L,R),A) :- A =< N,
AL is 2 * A, AR is AL + 1,
complete_binary_tree(N,L,AL),
complete_binary_tree(N,R,AR).
% ----------------------------------------------------------------------
% This was the solution to the exercise. What follows is an application
% of this result.
% We define a heap as a term heap(N,T) where N is the number of elements
% and T a complete binary tree (in the sense used above).
% The conservative usage of a heap is first to declare it with a predicate
% declare_heap/2 and then use it with a predicate element_at/3.
% declare_heap(H,N) :-
% declare H to be a heap with a fixed number N of elements
declare_heap(heap(N,T),N) :- complete_binary_tree(N,T).
% element_at(H,K,X) :- X is the element at address K in the heap H.
% The first element has address 1.
% (+,+,?)
element_at(heap(_,T),K,X) :-
binary_path(K,[],BP), element_at_path(T,BP,X).
binary_path(1,Bs,Bs) :- !.
binary_path(K,Acc,Bs) :- K > 1,
B is K /\ 1, K1 is K >> 1, binary_path(K1,[B|Acc],Bs).
element_at_path(t(X,_,_),[],X) :- !.
element_at_path(t(_,L,_),[0|Bs],X) :- !, element_at_path(L,Bs,X).
element_at_path(t(_,_,R),[1|Bs],X) :- element_at_path(R,Bs,X).
% We can transform lists into heaps and vice versa with the following
% useful predicate:
% list_heap(L,H) :- transform a list into a (limited) heap and vice versa.
list_heap(L,H) :- list(L), list_to_heap(L,H).
list_heap(L,heap(N,T)) :- integer(N), fill_list(heap(N,T),N,1,L).
list_to_heap(L,H) :-
length(L,N), declare_heap(H,N), fill_heap(H,L,1).
fill_heap(_,[],_).
fill_heap(H,[X|Xs],K) :- element_at(H,K,X), K1 is K+1, fill_heap(H,Xs,K1).
fill_list(_,N,K,[]) :- K > N.
fill_list(H,N,K,[X|Xs]) :- K =< N,
element_at(H,K,X), K1 is K+1, fill_list(H,N,K1,Xs).
% However, a more aggressive usage is *not* to define the heap in the
% beginning, but to use it as a partially instantiated data structure.
% Used in this way, the number of elements in the heap is unlimited.
% This is Power-Prolog!
% Try the following and find out exactly what happens.
% ?- element_at(H,5,alfa), element_at(H,2,beta), element(H,5,A).
%! \end{solution}Test your predicate in an appropriate way (e.g. pressing the northeast pointing arrow (↗) will load the code in a separate Prolog playground window). Layout a binary tree
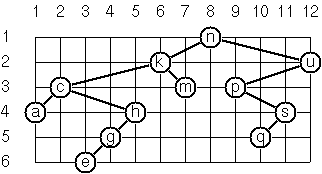
In this layout strategy, the position of a node v is obtained by the following two rules:
- x(v) is equal to the position of the node v in the inorder sequence
- y(v) is equal to the depth of the node v in the tree
:- module(_, _, [assertions]).
:- push_prolog_flag(multi_arity_warnings, off).
sorry :- throw(not_solved_yet).
:- test layout_binary_tree(T,PT) : (T = nil) => (PT = nil) + (not_fails, is_det).
:- test layout_binary_tree(T,PT) : (T = t(n,t(k,t(c,t(a,nil,nil),t(h,t(g,t(e,nil,nil),nil),nil)),t(m,nil,nil)),t(u,t(p,nil,t(s,t(q,nil,nil),nil)),nil))) => (PT = t(n,8,1,t(k,6,2,t(c,2,3,t(a,1,4,nil,nil),t(h,5,4,t(g,4,5,t(e,3,6,nil,nil),nil),nil)),t(m,7,3,nil,nil)),t(u,12,2,t(p,9,3,nil,t(s,11,4,t(q,10,5,nil,nil),nil)),nil))) + (not_fails, is_det).
add(X,nil,t(X,nil,nil)).
add(X,t(Root,L,R),t(Root,L1,R)) :- X @< Root, add(X,L,L1).
add(X,t(Root,L,R),t(Root,L,R1)) :- X @> Root, add(X,R,R1).
construct(L,T) :- construct(L,T,nil).
construct([],T,T).
construct([N|Ns],T,T0) :- add(N,T0,T1), construct(Ns,T,T1).
%! \begin{hint}
layout_binary_tree(T,PT) :- sorry.
% PT is the "positionned" binary
% tree obtained from the binary tree T. (+,?) or (?,+)
layout_binary_tree(T,PT,In,Out,D) :- sorry.
% T and PT as in layout_binary_tree/2;
% In is the position in the inorder sequence where the tree T (or PT)
% begins, Out is the position after the last node of T (or PT) in the
% inorder sequence. D is the depth of the root of T (or PT).
% (+,?,+,?,+) or (?,+,+,?,+)
%! \end{hint}
%! \begin{solution}
layout_binary_tree(T,PT) :- layout_binary_tree(T,PT,1,_,1).
layout_binary_tree(nil,nil,I,I,_).
layout_binary_tree(t(W,L,R),t(W,X,Y,PL,PR),Iin,Iout,Y) :-
Y1 is Y + 1,
layout_binary_tree(L,PL,Iin,X,Y1),
X1 is X + 1,
layout_binary_tree(R,PR,X1,Iout,Y1).
%! \end{solution}?- construct([n,k,m,c,a,h,g,e,u,p,s,q],T),layout_binary_tree(T,PT).
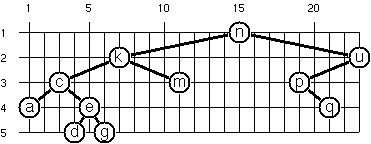
An alternative layout method is depicted in the illustration opposite. Find out the rules and write the corresponding Prolog predicate. Hint: On a given level, the horizontal distance between neighbouring nodes is constant.
:- module(_, _, [assertions]).
:- push_prolog_flag(multi_arity_warnings, off).
sorry :- throw(not_solved_yet).
:- test layout_binary_tree2(T,PT) : (T = nil) => (PT = nil) + (not_fails, is_det).
:- test layout_binary_tree2(T,PT) : (T = t(n,t(k,t(c,t(a,nil,nil),t(h,t(g,t(e,nil,nil),nil),nil)),t(m,nil,nil)),t(u,t(p,nil,t(s,t(q,nil,nil),nil)),nil))) => (PT = t(n,29,1,t(k,13,2,t(c,5,3,t(a,1,4,nil,nil),t(h,9,4,t(g,7,5,t(e,6,6,nil,nil),nil),nil)),t(m,21,3,nil,nil)),t(u,45,2,t(p,37,3,nil,t(s,41,4,t(q,39,5,nil,nil),nil)),nil))) + (not_fails, is_det).
add(X,nil,t(X,nil,nil)).
add(X,t(Root,L,R),t(Root,L1,R)) :- X @< Root, add(X,L,L1).
add(X,t(Root,L,R),t(Root,L,R1)) :- X @> Root, add(X,R,R1).
construct(L,T) :- construct(L,T,nil).
construct([],T,T).
construct([N|Ns],T,T0) :- add(N,T0,T1), construct(Ns,T,T1).
%! \begin{hint}
x_pos(T,X,D) :- sorry.
% X is the horizontal position of the root node of T
% with respect to the picture co-ordinate system. D is the horizontal
% distance between the root node of T and its successor(s) (if any).
% (+,-,+)
layout_binary_tree2(T,PT,X,Y,D) :- sorry.
% T and PT as in layout_binary_tree/2;
% D is the the horizontal distance between the root node of T and
% its successor(s) (if any). X, Y are the co-ordinates of the root node.
% (+,-,+,+,+)
hor_dist(T,D4) :- sorry.
% D4 is four times the horizontal distance between the
% root node of T and its successor(s) (if any).
% (+,-)
layout_binary_tree2(T,PT) :- sorry.
% PT is the "positionned" binary
% tree obtained from the binary tree T. (+,?)
%! \end{hint}
%! \begin{solution}
layout_binary_tree2(nil,nil) :- !.
layout_binary_tree2(T,PT) :-
hor_dist(T,D4), D is D4//4, x_pos(T,X,D),
layout_binary_tree2(T,PT,X,1,D).
hor_dist(nil,1).
hor_dist(t(_,L,R),D4) :-
hor_dist(L,D4L),
hor_dist(R,D4R),
max(D4L,D4R,M),
D4 is 2 * M.
max(X,Y,X):- X >= Y, !.
max(_X,Y,Y).
x_pos(t(_,nil,_),1,_) :- !.
x_pos(t(_,L,_),X,D) :- D2 is D//2, x_pos(L,XL,D2), X is XL+D.
layout_binary_tree2(nil,nil,_,_,_).
layout_binary_tree2(t(W,L,R),t(W,X,Y,PL,PR),X,Y,D) :-
Y1 is Y + 1,
Xleft is X - D,
D2 is D//2,
layout_binary_tree2(L,PL,Xleft,Y1,D2),
Xright is X + D,
layout_binary_tree2(R,PR,Xright,Y1,D2).
%! \end{solution}?- construct([n,k,m,c,a,e,d,g,u,p,q],T),layout_binary_tree2(T,PT).
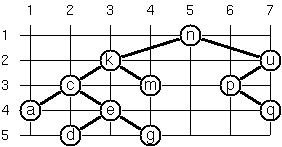
Yet another layout strategy is shown in the illustration opposite. The method yields a very compact layout while maintaining a certain symmetry in every node. Find out the rules and write the corresponding Prolog predicate. Use the same conventions as in Layout a binary tree (1) and (2) problems and test your predicate in an appropriate way. Note: This is a difficult problem. Don't give up too early! Which layout do you like most?
:- module(_, _, [assertions]).
sorry :- throw(not_solved_yet).
:- test layout_binary_tree3(T,PT) : (T = nil) => (PT = nil) + (not_fails, is_det).
:- test layout_binary_tree3(T,PT) : (T = t(n,t(k,t(c,t(a,nil,nil),t(h,t(g,t(e,nil,nil),nil),nil)),t(m,nil,nil)),t(u,t(p,nil,t(s,t(q,nil,nil),nil)),nil))) => (PT = t(n,5,1,t(k,3,2,t(c,2,3,t(a,1,4,nil,nil),t(h,3,4,t(g,2,5,t(e,1,6,nil,nil),nil),nil)),t(m,4,3,nil,nil)),t(u,7,2,t(p,6,3,nil,t(s,7,4,t(q,6,5,nil,nil),nil)),nil))) + (not_fails, is_det).
add(X,nil,t(X,nil,nil)).
add(X,t(Root,L,R),t(Root,L1,R)) :- X @< Root, add(X,L,L1).
add(X,t(Root,L,R),t(Root,L,R1)) :- X @> Root, add(X,R,R1).
construct(L,T) :- construct(L,T,nil).
construct([],T,T).
construct([N|Ns],T,T0) :- add(N,T0,T1), construct(Ns,T,T1).
%! \begin{hint}
layout_binary_tree3(T,PT) :- sorry.
% PT is the "positionned" binary
% tree obtained from the binary tree T. (+,?)
%! \end{hint}
%! \begin{solution}
layout_binary_tree3(nil,nil) :- !.
layout_binary_tree3(T,PT) :-
contour_tree(T,CT), % construct the "contour" tree CT
CT = t(_,_,_,Contour),
mincont(Contour,MC,0), % find the position of the leftmost node
Xroot is 1-MC,
layout_binary_tree3(CT,PT,Xroot,1).
contour_tree(nil,nil).
contour_tree(t(X,L,R),t(X,CL,CR,Contour)) :-
contour_tree(L,CL),
contour_tree(R,CR),
combine(CL,CR,Contour).
combine(nil,nil,[]).
combine(t(_,_,_,CL),nil,[c(-1,-1)|Cs]) :- shift(CL,-1,Cs).
combine(nil,t(_,_,_,CR),[c(1,1)|Cs]) :- shift(CR,1,Cs).
combine(t(_,_,_,CL),t(_,_,_,CR),[c(DL,DR)|Cs]) :-
maxdiff(CL,CR,MD,0),
DR is (MD+2)//2, DL is -DR,
merge(CL,CR,DL,DR,Cs).
shift([],_,[]).
shift([c(L,R)|Cs],S,[c(LS,RS)|CsS]) :-
LS is L+S, RS is R+S, shift(Cs,S,CsS).
maxdiff([],_,MD,MD) :- !.
maxdiff(_,[],MD,MD) :- !.
maxdiff([c(_,R1)|Cs1],[c(L2,_)|Cs2],MD,A) :-
Su is R1-L2,
max(A,Su,A1),
maxdiff(Cs1,Cs2,MD,A1).
max(X,Y,X):- X >= Y, !.
max(_X,Y,Y).
merge([],CR,_,DR,Cs) :- !, shift(CR,DR,Cs).
merge(CL,[],DL,_,Cs) :- !, shift(CL,DL,Cs).
merge([c(L1,_)|Cs1],[c(_,R2)|Cs2],DL,DR,[c(L,R)|Cs]) :-
L is L1+DL, R is R2+DR,
merge(Cs1,Cs2,DL,DR,Cs).
mincont([],MC,MC).
mincont([c(L,_)|Cs],MC,A) :-
min(A,L,A1),
mincont(Cs,MC,A1).
min(X,Y,X):- X < Y, !.
min(_X,Y,Y).
layout_binary_tree3(nil,nil,_,_).
layout_binary_tree3(t(W,nil,nil,_),t(W,X,Y,nil,nil),X,Y) :- !.
layout_binary_tree3(t(W,L,R,[c(DL,DR)|_]),t(W,X,Y,PL,PR),X,Y) :-
Y1 is Y + 1,
Xleft is X + DL,
layout_binary_tree3(L,PL,Xleft,Y1),
Xright is X + DR,
layout_binary_tree3(R,PR,Xright,Y1).
%! \end{solution}?- construct([n,k,m,c,a,e,d,g,u,p,q],T),layout_binary_tree3(T,PT).
String representation

Somebody represents binary trees as strings of the following type (see example opposite): a(b(d,e),c(,f(g,)))
[a)] Write a Prolog predicate which generates this string representation, if the tree is given as usual (as nil or t(X,L,R) term). Then write a predicate which does this inverse; i.e. given the string representation, construct the tree in the usual form. Finally, combine the two predicates in a single predicate tree_string/2 which can be used in both directions.
:- module(_, _, [assertions]).
:- use_module(library(classic/classic_predicates),[append/3, atom_chars/2]).
:- push_prolog_flag(multi_arity_warnings, off).
sorry :- throw(not_solved_yet).
:- test tree_string(T,ST) : (T = nil) => (ST = '') + (not_fails, is_det).
:- test tree_string(T,ST) : (T = t(x, t(x, t(x, nil, nil), t(x, nil, nil)), t(x, t(x, nil, nil),t(x, nil, nil)))) => (PT = 'x(x(x,x),x(x,x))') + (not_fails, is_det).
%! \begin{hint}
% The string representation has the following syntax:
%
% <tree> ::= | <letter><subtrees>
%
% <subtrees> ::= | '(' <tree> ',' <tree> ')'
%
% According to this syntax, a leaf node (with letter x) could
% be represented by x(,) and not only by the single character x.
% However, we will avoid this when generating the string
% representation.
tree_string(T,S) :- sorry.
%! \end{hint}
%! \begin{solution}
tree_string(T,S) :- nonvar(T), !, tree_to_string(T,S).
tree_string(T,S) :- nonvar(S), string_to_tree(S,T).
tree_to_string(T,S) :- tree_to_list(T,L), atom_chars(S,L).
tree_to_list(nil,[]).
tree_to_list(t(X,nil,nil),[X]) :- !.
tree_to_list(t(X,L,R),[X,'('|List]) :-
tree_to_list(L,LsL),
tree_to_list(R,LsR),
append(LsL,[','],List1),
append(List1,LsR,List2),
append(List2,[')'],List).
string_to_tree(S,T) :- atom_chars(S,L), list_to_tree(L,T).
list_to_tree([],nil).
list_to_tree([X],t(X,nil,nil)) :- character_code(X).
list_to_tree([X,'('|List],t(X,Left,Right)) :- character_code(X),
append(List1,[')'],List),
append(LeftList,[','|RightList],List1),
list_to_tree(LeftList,Left),
list_to_tree(RightList,Right).
%! \end{solution}?- tree_string(t(n,t(k,t(c,t(a,nil,nil),t(h,t(g,t(e,nil,nil),nil),nil)),t(m,nil,nil)),t(u,t(p,nil,t(s,t(q,nil,nil),nil)),nil)),A).[b)] Write the same predicate tree_string/2 using difference lists and a single predicate tree_dlist/2 which does the conversion between a tree and a difference list in both directions. For simplicity, suppose the information in the nodes is a single letter and there are no spaces in the string.
:- module(_, _, [assertions]).
:- use_module(library(classic/classic_predicates),[append/3, atom_chars/2]).
:- push_prolog_flag(multi_arity_warnings, off).
sorry :- throw(not_solved_yet).
:- test tree_string(T,ST) : (T = nil) => (ST = '') + (not_fails, is_det).
:- test tree_string(T,ST) : (T = t(x, t(x, t(x, nil, nil), t(x, nil, nil)), t(x, t(x, nil, nil),t(x, nil, nil)))) => (PT = 'x(x(x,x),x(x,x))') + (not_fails, is_det).
%! \begin{hint}
tree_string(T,S) :- sorry.
%! \end{hint}
%! \begin{solution}
% Most elegant solution using difference lists.
tree_string(T,S) :- nonvar(T), tree_dlist(T,L-[]), !, atom_chars(S,L).
tree_string(T,S) :- nonvar(S), atom_chars(S,L), tree_dlist(T,L-[]).
% tree_dlist/2 does the trick in both directions!
tree_dlist(nil,L-L).
tree_dlist(t(X,nil,nil),L1-L2) :-
letter(X,L1-L2).
tree_dlist(t(X,Left,Right),L1-L7) :-
letter(X,L1-L2),
symbol('(',L2-L3),
tree_dlist(Left,L3-L4),
symbol(',',L4-L5),
tree_dlist(Right,L5-L6),
symbol(')',L6-L7).
symbol(X,[X|Xs]-Xs).
letter(X,L1-L2) :- symbol(X,L1-L2).
%! \end{solution}?- tree_string(t(n,t(k,t(c,t(a,nil,nil),t(h,t(g,t(e,nil,nil),nil),nil)),t(m,nil,nil)),t(u,t(p,nil,t(s,t(q,nil,nil),nil)),nil)),A).
Preorder and inorder
[a)] Write predicates preorder/2 and inorder/2 that construct the preorder and inorder sequence of a given binary tree, respectively. The results should be atoms, e.g. 'abdecfg' for the preorder sequence of the example in String representation of binary trees problem.
:- module(_, _, [assertions]).
:- use_module(library(classic/classic_predicates),[append/3, atom_chars/2]).
sorry :- throw(not_solved_yet).
:- test preorder(T,S) : (T = nil) => (S = '') + (not_fails, is_det).
:- test preorder(T,S) : (T = t(n,t(k,t(c,t(a,nil,nil),t(h,t(g,t(e,nil,nil),nil),nil)),t(m,nil,nil)),t(u,t(p,nil,t(s,t(q,nil,nil),nil)),nil))) => (S = nkcahgemupsq) + (not_fails, is_det).
%! \begin{hint}
preorder(T,S) :- sorry.
%! \end{hint}
%! \begin{solution}
preorder(T,S) :- preorder_tl(T,L), atom_chars(S,L).
preorder_tl(nil,[]).
preorder_tl(t(X,Left,Right),[X|List]) :-
preorder_tl(Left,ListLeft),
preorder_tl(Right,ListRight),
append(ListLeft,ListRight,List).
inorder(T,S) :- inorder_tl(T,L), atom_chars(S,L).
inorder_tl(nil,[]).
inorder_tl(t(X,Left,Right),List) :-
inorder_tl(Left,ListLeft),
inorder_tl(Right,ListRight),
append(ListLeft,[X|ListRight],List).
%! \end{solution}?- preorder(t(n,t(k,t(c,t(a,nil,nil),t(h,t(g,t(e,nil,nil),nil),nil)),t(m,nil,nil)),t(u,t(p,nil,t(s,t(q,nil,nil),nil)),nil)),A).[b)] Can you use preorder/2 from problem part a) in the reverse direction; i.e. given a preorder sequence, construct a corresponding tree? If not, make the necessary arrangements.
:- module(_, _, [assertions]).
:- use_module(library(classic/classic_predicates),[append/3, atom_chars/2]).
sorry :- throw(not_solved_yet).
:- test preorder(T,S) : (T = nil) => (S = '') + (not_fails, is_det).
:- test preorder(T,S) : (T = t(n,t(k,t(c,t(a,nil,nil),t(h,t(g,t(e,nil,nil),nil),nil)),t(m,nil,nil)),t(u,t(p,nil,t(s,t(q,nil,nil),nil)),nil))) => (S = nkcahgemupsq) + (not_fails, is_det).
:- test inorder(T,S) : (T = nil) => (S = '') + (not_fails, is_det).
:- test inorder(T,S) : (T = t(n,t(k,t(c,t(a,nil,nil),t(h,t(g,t(e,nil,nil),nil),nil)),t(m,nil,nil)),t(u,t(p,nil,t(s,t(q,nil,nil),nil)),nil))) => (S = aceghkmnpqsu) + (not_fails, is_det).
%! \begin{hint}
inorder(T,S) :- sorry.
% S is the inorder tre traversal sequence of the
% nodes of the binary tree T. (tree,atom) (+,?) or (?,+)
preorder(T,S) :- sorry.
% S is the preorder tre traversal sequence of the
% nodes of the binary tree T. (tree,atom) (+,?) or (?,+)
%! \end{hint}
%! \begin{solution}
preorder(T,S) :- nonvar(T), !, preorder_tl(T,L), atom_chars(S,L).
preorder(T,S) :- atom(S), atom_chars(S,L), preorder_lt(T,L).
preorder_tl(nil,[]).
preorder_tl(t(X,Left,Right),[X|List]) :-
preorder_tl(Left,ListLeft),
preorder_tl(Right,ListRight),
append(ListLeft,ListRight,List).
preorder_lt(nil,[]).
preorder_lt(t(X,Left,Right),[X|List]) :-
append(ListLeft,ListRight,List),
preorder_lt(Left,ListLeft),
preorder_lt(Right,ListRight).
inorder(T,S) :- nonvar(T), !, inorder_tl(T,L), atom_chars(S,L).
inorder(T,S) :- atom(S), atom_chars(S,L), inorder_lt(T,L).
inorder_tl(nil,[]).
inorder_tl(t(X,Left,Right),List) :-
inorder_tl(Left,ListLeft),
inorder_tl(Right,ListRight),
append(ListLeft,[X|ListRight],List).
inorder_lt(nil,[]).
inorder_lt(t(X,Left,Right),List) :-
append(ListLeft,[X|ListRight],List),
inorder_lt(Left,ListLeft),
inorder_lt(Right,ListRight).
%! \end{solution}?- preorder(t(n,t(k,t(c,t(a,nil,nil),t(h,t(g,t(e,nil,nil),nil),nil)),t(m,nil,nil)),t(u,t(p,nil,t(s,t(q,nil,nil),nil)),nil)),A).
?- inorder(t(n,t(k,t(c,t(a,nil,nil),t(h,t(g,t(e,nil,nil),nil),nil)),t(m,nil,nil)),t(u,t(p,nil,t(s,t(q,nil,nil),nil)),nil)),A).[c)] If both the preorder sequence and the inorder sequence of the nodes of a binary tree are given, then the tree is determined unambiguously. Write a predicate pre_in_tree/3 that does the job.
:- module(_, _, [assertions]).
:- use_module(library(classic/classic_predicates),[append/3, atom_chars/2]).
sorry :- throw(not_solved_yet).
:- test pre_in_tree(A,B,C) : (A = abc, B = bca) => (C = t(a,t(b,nil,t(c,nil,nil)),nil)) + (not_fails, is_det).
preorder(T,S) :- nonvar(T), !, preorder_tl(T,L), atom_chars(S,L).
preorder(T,S) :- atom(S), atom_chars(S,L), preorder_lt(T,L).
preorder_tl(nil,[]).
preorder_tl(t(X,Left,Right),[X|List]) :-
preorder_tl(Left,ListLeft),
preorder_tl(Right,ListRight),
append(ListLeft,ListRight,List).
preorder_lt(nil,[]).
preorder_lt(t(X,Left,Right),[X|List]) :-
append(ListLeft,ListRight,List),
preorder_lt(Left,ListLeft),
preorder_lt(Right,ListRight).
inorder(T,S) :- nonvar(T), !, inorder_tl(T,L), atom_chars(S,L).
inorder(T,S) :- atom(S), atom_chars(S,L), inorder_lt(T,L).
inorder_tl(nil,[]).
inorder_tl(t(X,Left,Right),List) :-
inorder_tl(Left,ListLeft),
inorder_tl(Right,ListRight),
append(ListLeft,[X|ListRight],List).
inorder_lt(nil,[]).
inorder_lt(t(X,Left,Right),List) :-
append(ListLeft,[X|ListRight],List),
inorder_lt(Left,ListLeft),
inorder_lt(Right,ListRight).
%! \begin{hint}
pre_in_tree(P,I,T) :- sorry.
% T is the binary tree that has the preorder
% sequence P and inorder sequence I.
% (atom,atom,tree) (+,+,?)
%! \end{hint}
%! \begin{solution}
pre_in_tree(P,I,T) :- preorder(T,P), inorder(T,I).
% This is a nice application of the generate-and-test method.
% We can push the tester inside the generator in order to get
% a (much) better performance.
pre_in_tree_push(P,I,T) :-
atom_chars(P,PL), atom_chars(I,IL), pre_in_tree_pu(PL,IL,T).
pre_in_tree_pu([],[],nil).
pre_in_tree_pu([X|PL],IL,t(X,Left,Right)) :-
append(ILeft,[X|IRight],IL),
append(PLeft,PRight,PL),
pre_in_tree_pu(PLeft,ILeft,Left),
pre_in_tree_pu(PRight,IRight,Right).
% Nice. But there is a still better solution. See problem d)!
%! \end{solution}?- pre_in_tree(abc,bca,B).[d)] Solve problems a) to c) using difference lists. Cool! Use the predefined predicate time/1 to compare the solutions.
:- module(_, _, [assertions]).
:- use_module(library(classic/classic_predicates),[atom_chars/2]).
sorry :- throw(not_solved_yet).
:- test pre_in_tree_d(A,B,C) : (A = abc, B = bca) => (C = t(a,t(b,nil,t(c,nil,nil)),nil)) + (not_fails, is_det).
%! \begin{hint}
pre_in_tree_d(P,I,T) :- sorry.
% T is the binary tree that has the preorder
% sequence P and inorder sequence I.
% (atom,atom,tree) (+,+,?)
%! \end{hint}
%! \begin{solution}
pre_in_tree_d(P,I,T) :-
atom_chars(P,PL), atom_chars(I,IL), pre_in_tree_dl(PL-[],IL-[],T).
pre_in_tree_dl(P-P,I-I,nil).
pre_in_tree_dl(P1-P4,I1-I4,t(X,Left,Right)) :-
symbol(X,P1-P2), symbol(X,I2-I3),
pre_in_tree_dl(P2-P3,I1-I2,Left),
pre_in_tree_dl(P3-P4,I3-I4,Right).
symbol(X,[X|Xs]-Xs).
% Isn't it cool? But the best of it is the performance!
% With the generate-and-test solution (p68c):
% ?- time(pre_in_tree(abdecfg,dbeacgf,_)).
% 9,048 inferences in 0.01 seconds (904800 Lips)
% With the "pushed" generate-and-test solution (p68c):
% ?- time(pre_in_tree_push(abdecfg,dbeacgf,_)).
% 67 inferences in 0.00 seconds (Infinite Lips)
% With the difference list solution (p68d):
% ?- time(pre_in_tree_d(abdecfg,dbeacgf,_)).
% 32 inferences in 0.00 seconds (Infinite Lips)
% Note that the predicate pre_in_tree_dl/3 runs in almost any
% flow pattern. Try it out!
%! \end{solution}What happens if the same character appears in more than one node. Try for instance: ?- pre_in_tree_d(aba,baa,T).
Dotstring representation
:- module(_, _, [assertions]).
:- use_module(library(classic/classic_predicates),[atom_chars/2]).
sorry :- throw(not_solved_yet).
:- test tree_dotstring(A,B) : (B = 'abd..e..c.fg...') => (A = t(a,t(b,t(d,nil,nil),t(e,nil,nil)),t(c,nil,t(f,t(g,nil,nil),nil)))) + (not_fails, is_det).
:- test tree_dotstring(A,B) : (A = nil) => (B = '.') + (not_fails, is_det).
%! \begin{hint}
% The syntax of the dotstring representation is super simple:
%
% <tree> ::= . | <letter> <tree> <tree>
tree_dotstring(T,S) :- sorry.
%! \end{hint}
%! \begin{solution}
tree_dotstring(T,S) :- nonvar(T), !, tree_dots_dl(T,L-[]), atom_chars(S,L).
tree_dotstring(T,S) :- atom(S), atom_chars(S,L), tree_dots_dl(T,L-[]).
tree_dots_dl(nil,L1-L2) :- symbol('.',L1-L2).
tree_dots_dl(t(X,Left,Right),L1-L4) :-
letter(X,L1-L2),
tree_dots_dl(Left,L2-L3),
tree_dots_dl(Right,L3-L4).
symbol(X,[X|Xs]-Xs).
letter(X,L1-L2) :- symbol(X,L1-L2).
%! \end{solution}?- tree_dotstring(A,'abd..e..c.fg...').
Multiway Trees
A multiway tree is composed of a root element and a (possibly empty) set of successors which are multiway trees themselves. A multiway tree is never empty. The set of successor trees is sometimes called a forest.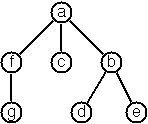
In Prolog we represent a multiway tree by a term t(X,F), where X denotes the root node and F denotes the forest of successor trees (a Prolog list). The example tree depicted opposite is therefore represented by the following Prolog term:
T = t(a,[t(f,[t(g,[])]),t(c,[]),t(b,[t(d,[]),t(e,[])])])
Is it a multiway tree?
:- module(_, _, [assertions]).
sorry :- throw(not_solved_yet).
:- test istree(A) : (A = t(a,[t(f,[t(g,[])]),t(c,[]),t(b,[t(d,[]),t(e,[])])])) + (not_fails, is_det).
:- test istree(A) : (A = t(_,[])) + (not_fails, is_det).
%! \begin{hint}
istree(T) :- sorry.
% T is a term representing a multiway tree (i), (o)
%! \end{hint}
%! \begin{solution}
istree(t(_,F)) :- isforest(F).
isforest([]).
isforest([T|Ts]) :- istree(T), isforest(Ts).
%! \end{solution}?- istree(t(a,[t(f,[t(g,[])]),t(c,[]),t(b,[t(d,[]),t(e,[])])])).
Number of nodes
:- module(_, _, [assertions]).
:- use_module(library(classic/classic_predicates), [between/3]).
sorry :- throw(not_solved_yet).
:- test nnodes(A,N) : (A = t(a,[t(f,[])])) => (N = 2) + (not_fails, is_det).
%! \begin{hint}
nnodes(T,N) :- sorry.
% the multiway tree T has N nodes (i,o))
%! \end{hint}
%! \begin{solution}
nnodes(t(_,F),N) :- nnodes(F,NF), N is NF+1.
nnodes([],0).
nnodes([T|Ts],N) :- nnodes(T,NT), nnodes(Ts,NTs), N is NT+NTs.
% Note that nnodes is called for trees and forests. An early
% form of polymorphism!
% For the flow pattern (o,i) we can write:
nnodes2(t(_,F),N) :- N > 0, NF is N-1, nnodes2F(F,NF).
nnodes2F([],0).
nnodes2F([T|Ts],N) :- N > 0,
between(1,N,NT), nnodes2(T,NT),
NTs is N-NT, nnodes2F(Ts,NTs).
%! \end{solution}?- nnodes(t(a,[t(f,[])]),N).
Tree construction
By this rule, the tree in the figure opposite is represented as: afg^^c^bd^e^^^
Define the syntax of the string and write a predicate tree(String,Tree) to construct the Tree when the String is given. Work with atoms (instead of strings). Make your predicate work in both directions.
:- module(_, _, [assertions]).
:- use_module(library(classic/classic_predicates), [append/3, atom_chars/2]).
sorry :- throw(not_solved_yet).
:- test tree(A,B) : (B = t(a,[t(f,[t(g,[])]),t(c,[]),t(b,[t(d,[]),t(e,[])])])) => (A = 'afg^^c^bd^e^^^') + (not_fails, is_det).
%! \begin{hint}
% Syntax in BNF:
% <tree> ::= <letter> <forest> '^'
% <forest> ::= | <tree> <forest>
tree(TS,T) :- sorry.
%! \end{hint}
%! \begin{solution}
% First a nice solution using difference lists
tree(TS,T) :- atom(TS), !, atom_chars(TS,TL), tree_d(TL-[],T). % (+,?)
tree(TS,T) :- nonvar(T), tree_d(TL-[],T), atom_chars(TS,TL). % (?,+)
tree_d([X|F1]-T, t(X,F)) :- forest_d(F1-['^'|T],F).
forest_d(F-F,[]).
forest_d(F1-F3,[T|F]) :- tree_d(F1-F2,T), forest_d(F2-F3,F).
% Another solution, not as elegant as the previous one.
tree_2(TS,T) :- atom(TS), !, atom_chars(TS,TL), tree_a(TL,T). % (+,?)
tree_2(TS,T) :- nonvar(T), tree_a(TL,T), atom_chars(TS,TL). % (?,+)
tree_a(TL,t(X,F)) :-
append([X],FL,L1), append(L1,['^'],TL), forest_a(FL,F).
forest_a([],[]).
forest_a(FL,[T|Ts]) :- append(TL,TsL,FL),
tree_a(TL,T), forest_a(TsL,Ts).
%! \end{solution}?- tree(A,t(a,[t(f,[t(g,[])]),t(c,[]),t(b,[t(d,[]),t(e,[])])])).
Internal path
:- module(_, _, [assertions]).
:- push_prolog_flag(multi_arity_warnings, off).
sorry :- throw(not_solved_yet).
:- test ipl(A,B) : (A = t(a,[t(f,[t(g,[])]),t(c,[]),t(b,[t(d,[]),t(e,[])])])) => (B = 9)+ (not_fails, is_det).
%! \begin{hint}
ipl(Tree,L) :- sorry.
% L is the internal path length of the tree Tree
% (multiway-tree, integer) (+,?)
%! \end{hint}
%! \begin{solution}
ipl(T,L) :- ipl(T,0,L).
ipl(t(_,F),D,L) :- D1 is D+1, ipl(F,D1,LF), L is LF+D.
ipl([],_,0).
ipl([T1|Ts],D,L) :- ipl(T1,D,L1), ipl(Ts,D,Ls), L is L1+Ls.
% Notice the polymorphism: ipl is called with trees and with forests
% as first argument.
%! \end{solution}?- ipl(t(a,[t(f,[t(g,[])]),t(c,[]),t(b,[t(d,[]),t(e,[])])]),B).
Bottom-up order sequence
:- module(_, _, [assertions]).
:- use_module(library(classic/classic_predicates), [append/3]).
:- push_prolog_flag(multi_arity_warnings, off).
sorry :- throw(not_solved_yet).
:- test bottom_up(A,B) : (A = t(a,[t(f,[t(g,[])]),t(c,[]),t(b,[t(d,[]),t(e,[])])])) => (B = [g,f,c,d,e,b,a])+ (not_fails, is_det).
%! \begin{hint}
bottom_up(Tree,Seq) :- sorry.
% Seq is the bottom-up sequence of the nodes of
% the multiway tree Tree. (+,?)
%! \end{hint}
%! \begin{solution}
bottom_up_f(t(X,F),Seq) :-
bottom_up_f(F,SeqF), append(SeqF,[X],Seq).
bottom_up_f([],[]).
bottom_up_f([T|Ts],Seq):-
bottom_up_f(T,SeqT), bottom_up_f(Ts,SeqTs), append(SeqT,SeqTs,Seq).
% The predicate bottom_up/2 produces a stack overflow when called
% in the (-,+) flow pattern. There are two problems with that.
% First, the polymorphism does not work properly, because during
% decomposing the string, the program cannot guess whether it should
% construct a tree or a forest next. We can fix this using two
% separate predicates bottom_up_tree/2 and bottom_up_forset/2.
% Secondly, if we maintain the order of the subgoals, then
% the interpreter falls into an endless loop after finding the
% first solution. We can fix this by changing the order of the
% goals as follows:
bottom_up_tree(t(X,F),Seq) :-
append(SeqF,[X],Seq), bottom_up_forest(F,SeqF).
bottom_up_forest([],[]).
bottom_up_forest([T|Ts],Seq):-
append(SeqT,SeqTs,Seq),
bottom_up_tree(T,SeqT), bottom_up_forest(Ts,SeqTs).
% Unfortunately, this version doesn't run in both directions either.
% In order to have a predicate which runs forward and backward, we
% have to determine the flow pattern and then call one of the above
% predicates, as follows:
bottom_up(T,Seq) :- nonvar(T), !, bottom_up_f(T,Seq).
bottom_up(T,Seq) :- nonvar(Seq), bottom_up_tree(T,Seq).
% This is not very elegant, I agree.
%! \end{solution}?- bottom_up(t(a,[t(f,[t(g,[])]),t(c,[]),t(b,[t(d,[]),t(e,[])])]),B).
Lisp-like tree representation
The following pictures show how multiway tree structures are represented in Lisp.
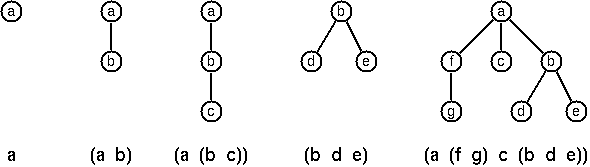
Note that in the "lispy" notation a node with successors (children) in the tree is always the first element in a list, followed by its children. The "lispy" representation of a multiway tree is a sequence of atoms and parentheses ( and ), which we shall collectively call "tokens". We can represent this sequence of tokens as a Prolog list; e.g. the lispy expression (a (b c)) could be represented as the Prolog list ['(', a, '(', b, c, ')', ')']. Write a predicate tree_ltl(T,LTL) which constructs the "lispy token list" LTL if the tree is given as term T in the usual Prolog notation.
:- module(_, _, [assertions]).
:- use_module(library(classic/classic_predicates), [append/3]).
:- push_prolog_flag(multi_arity_warnings, off).
sorry :- throw(not_solved_yet).
:- test tree_ltl(A,B) :(B = ['(', a, '(', b, c, ')', ')']) => (A = t(a,[t(b,[t(c,[])])])) + (not_fails, is_det).
%! \begin{hint}
tree_ltl(T,L) :- sorry.
% L is the "lispy token list" of the multiway tree T
%! \end{hint}
%! \begin{solution}
tree_ltl(T,L) :- tree_ltl_d(T,L-[]).
% using difference lists
tree_ltl_d(t(X,[]),[X|L]-L) :- X \= '('.
tree_ltl_d(t(X,[T|Ts]),['(',X|L]-R) :- forest_ltl_d([T|Ts],L-[')'|R]).
forest_ltl_d([],L-L).
forest_ltl_d([T|Ts],L-R) :- tree_ltl_d(T,L-M), forest_ltl_d(Ts,M-R).
%! \end{solution}?- tree_ltl(A,['(', a, '(', b, c, ')', ')']).As a second, even more interesting exercise try to rewrite tree_ltl/2 in a way that the inverse conversion is also possible: Given the list LTL, construct the Prolog tree T. Use difference lists. Graphs
A graph is defined as a set of nodes and a set of edges, where each edge is a pair of nodes. There are several ways to represent graphs in Prolog. One method is to represent each edge separately as one clause (fact). In this form, the graph depicted below is represented as the following predicate:
edge(h,g). edge(k,f). edge(f,b). ...We call this edge-clause form. Obviously, isolated nodes cannot be represented. Another method is to represent the whole graph as one data object. According to the definition of the graph as a pair of two sets (nodes and edges), we may use the following Prolog term to represent the example graph:
graph([b,c,d,f,g,h,k],[e(b,c),e(b,f),e(c,f),e(f,k),e(g,h)])We call this graph-term form. Note, that the lists are kept sorted, they are really sets, without duplicated elements. Each edge appears only once in the edge list; i.e. an edge from a node x to another node y is represented as e(x,y), the term e(y,x) is not present. The graph-term form is our default representation. In Ciao Prolog there are predefined predicates to work with sets.
A third representation method is to associate with each node the set of nodes that are adjacent to that node. We call this the adjacency-list form. In our example:
[n(b,[c,f]), n(c,[b,f]), n(d,[]), n(f,[b,c,k]), ...]The representations we introduced so far are Prolog terms and therefore well suited for automated processing, but their syntax is not very user-friendly. Typing the terms by hand is cumbersome and error-prone. We can define a more compact and "human-friendly" notation as follows: A graph is represented by a list of atoms and terms of the type X-Y (i.e. functor - and arity 2). The atoms stand for isolated nodes, the X-Y terms describe edges. If an X appears as an endpoint of an edge, it is automatically defined as a node. Our example could be written as:
[b-c, f-c, g-h, d, f-b, k-f, h-g]We call this the human-friendly form. As the example shows, the list does not have to be sorted and may even contain the same edge multiple times. Notice the isolated node d. (Actually, isolated nodes do not even have to be atoms in the Prolog sense, they can be compound terms, as in d(3.75,blue) instead of d in the example).
When the edges are directed we call them arcs. These are represented by ordered pairs. Such a graph is called directed graph. To represent a directed graph, the forms discussed above are slightly modified. The example graph opposite is represented as follows:
- Arc-clause form:
arc(s,u). arc(u,r). ...
- Graph-term form:
digraph([r,s,t,u,v],[a(s,r),a(s,u),a(u,r),a(u,s),a(v,u)])
- Adjacency-list form:
[n(r,[]),n(s,[r,u]),n(t,[]),n(u,[r]),n(v,[u])]Note that the adjacency-list does not have the information on whether it is a graph or a digraph.
- Human-friendly form:
[s > r, t, u > r, s > u, u > s, v > u]Finally, graphs and digraphs may have additional information attached to nodes and edges (arcs). For the nodes, this is no problem, as we can easily replace the single character identifiers with arbitrary compound terms, such as city('London',4711). On the other hand, for edges we have to extend our notation. Graphs with additional information attached to edges are called labelled graphs.
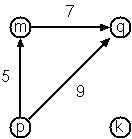
- Arc-clause form:
arc(m,q,7). arc(p,q,9). arc(p,m,5).
- Graph-term form:
digraph([k,m,p,q],[a(m,p,7),a(p,m,5),a(p,q,9)])
- Adjacency-list form:
[n(k,[]),n(m,[q/7]),n(p,[m/5,q/9]),n(q,[])]Notice how the edge information has been packed into a term with functor / and arity 2, together with the corresponding node.
- Human-friendly form:
[p>q/9, m>q/7, k, p>m/5]The notation for labelled graphs can also be used for so-called multi-graphs, where more than one edge (or arc) are allowed between two given nodes.
Conversions
:- module(_, _, [assertions]).
:- use_module(library(idlists), [memberchk/2]).
:- use_module(library(sort)).
:- use_module(library(aggregates), [findall/3]).
:- use_module(library(classic/classic_predicates), [delete/3]).
:- data edge/2.
:- data arc/2.
:- test alist_gterm(Type,AL,G1) : (Type = graph, AL = [n(b,[c,f]),n(c,[b,f]),n(d,[]),n(f,[b,c,k]),n(g,[h]),n(h,[g]),n(k,[f])]) => (G1 = graph([b,c,d,f,g,h,k],[e(b,c),e(b,f),e(c,f),e(f,k),e(g,h)]))+ (not_fails, is_det).
:- test alist_gterm(Type,AL,G1) : (Type = graph, AL = [n(t,[]),n(s>r,[]),n(s>u,[]),n(u>r,[]),n(u>s,[]),n(v>u,[])]) => (G1 = graph([t,s>r,s>u,u>r,u>s,v>u],[])) + (not_fails, is_det).
:- test alist_gterm(Type,AL,G1) : (Type = graph, AL = []) => (G1 = graph([],[])) + (not_fails, is_det).
sorry :- throw(not_solved_yet).
%! \begin{hint}
% We use the following notation:
%
% adjacency-list (alist): [n(b,[c,g,h]), n(c,[b,d,f,h]), n(d,[c,f]), ...]
%
% graph-term (gterm) graph([b,c,d,f,g,h,k],[e(b,c),e(b,g),e(b,h), ...]) or
% digraph([r,s,t,u],[a(r,s),a(r,t),a(s,t), ...])
%
% edge-clause (ecl): edge(b,g). (in program database)
% arc-clause (acl): arc(r,s). (in program database)
%
% human-friendly (hf): [a-b,c,g-h,d-e] or [a>b,h>g,c,b>a]
%
% The main conversion predicates are: alist_gterm/3 and human_gterm/2 which
% both (hopefully) work in either direction and for graphs as well as
% for digraphs, labelled or not.
alist_gterm(Type,AL,GT) :- sorry.
% convert between adjacency-list and graph-term
% representation. Type is either 'graph' or 'digraph'.
% (atom,alist,gterm) (+,+,?) or (?,?,+)
%! \end{hint}
%! \begin{solution}
alist_gterm(Type,AL,GT):- nonvar(GT), !, gterm_to_alist(GT,Type,AL).
alist_gterm(Type,AL,GT):- atom(Type), nonvar(AL), alist_to_gterm(Type,AL,GT).
gterm_to_alist(graph(Ns,Es),graph,AL) :- memberchk(e(_,_,_),Es), ! ,
lgt_al(Ns,Es,AL).
gterm_to_alist(graph(Ns,Es),graph,AL) :- !,
gt_al(Ns,Es,AL).
gterm_to_alist(digraph(Ns,As),digraph,AL) :- memberchk(a(_,_,_),As), !,
ldt_al(Ns,As,AL).
gterm_to_alist(digraph(Ns,As),digraph,AL) :-
dt_al(Ns,As,AL).
% labelled graph
lgt_al([],_,[]).
lgt_al([V|Vs],Es,[n(V,L)|Ns]) :-
findall(T,((member(e(X,V,I),Es) ; member(e(V,X,I),Es)),T = X/I),L),
lgt_al(Vs,Es,Ns).
% unlabelled graph
gt_al([],_,[]).
gt_al([V|Vs],Es,[n(V,L)|Ns]) :-
findall(X,(member(e(X,V),Es) ; member(e(V,X),Es)),L), gt_al(Vs,Es,Ns).
% labelled digraph
ldt_al([],_,[]).
ldt_al([V|Vs],As,[n(V,L)|Ns]) :-
findall(T,(member(a(V,X,I),As), T=X/I),L), ldt_al(Vs,As,Ns).
% unlabelled digraph
dt_al([],_,[]).
dt_al([V|Vs],As,[n(V,L)|Ns]) :-
findall(X,member(a(V,X),As),L), dt_al(Vs,As,Ns).
alist_to_gterm(graph,AL,graph(Ns,Es)) :- !, al_gt(AL,Ns,EsU,[]), sort(EsU,Es).
alist_to_gterm(digraph,AL,digraph(Ns,As)) :- al_dt(AL,Ns,AsU,[]), sort(AsU,As).
al_gt([],[],Es,Es).
al_gt([n(V,Xs)|Ns],[V|Vs],Es,Acc) :-
add_edges(V,Xs,Acc1,Acc), al_gt(Ns,Vs,Es,Acc1).
add_edges(_,[],Es,Es).
add_edges(V,[X/_|Xs],Es,Acc) :- V @> X, !, add_edges(V,Xs,Es,Acc).
add_edges(V,[X|Xs],Es,Acc) :- V @> X, !, add_edges(V,Xs,Es,Acc).
add_edges(V,[X/I|Xs],Es,Acc) :- V @=< X, !, add_edges(V,Xs,Es,[e(V,X,I)|Acc]).
add_edges(V,[X|Xs],Es,Acc) :- V @=< X, add_edges(V,Xs,Es,[e(V,X)|Acc]).
al_dt([],[],As,As).
al_dt([n(V,Xs)|Ns],[V|Vs],As,Acc) :-
add_arcs(V,Xs,Acc1,Acc), al_dt(Ns,Vs,As,Acc1).
add_arcs(_,[],As,As).
add_arcs(V,[X/I|Xs],As,Acc) :- !, add_arcs(V,Xs,As,[a(V,X,I)|Acc]).
add_arcs(V,[X|Xs],As,Acc) :- add_arcs(V,Xs,As,[a(V,X)|Acc]).
% ---------------------------------------------------------------------------
% ecl_to_gterm(GT) :- construct a graph-term from edge/2 facts in the
% program database.
ecl_to_gterm(GT) :-
findall(E,(edge(X,Y),E=X-Y),Es), human_gterm(Es,GT).
% acl_to_gterm(GT) :- construct a graph-term from arc/2 facts in the
% program database.
acl_to_gterm(GT) :-
findall(A,(arc(X,Y),A= >(X,Y)),As), human_gterm(As,GT).
% ---------------------------------------------------------------------------
% human_gterm(HF,GT) :- convert between human-friendly and graph-term
% representation.
% (list,gterm) (+,?) or (?,+)
human_gterm(HF,GT):- nonvar(GT), !, gterm_to_human(GT,HF).
human_gterm(HF,GT):- nonvar(HF), human_to_gterm(HF,GT).
gterm_to_human(graph(Ns,Es),HF) :- memberchk(e(_,_,_),Es), !,
lgt_hf(Ns,Es,HF).
gterm_to_human(graph(Ns,Es),HF) :- !,
gt_hf(Ns,Es,HF).
gterm_to_human(digraph(Ns,As),HF) :- memberchk(a(_,_,_),As), !,
ldt_hf(Ns,As,HF).
gterm_to_human(digraph(Ns,As),HF) :-
dt_hf(Ns,As,HF).
% labelled graph
lgt_hf(Ns,[],Ns).
lgt_hf(Ns,[e(X,Y,I)|Es],[X-Y/I|Hs]) :-
delete(Ns,X,Ns1),
delete(Ns1,Y,Ns2),
lgt_hf(Ns2,Es,Hs).
% unlabelled graph
gt_hf(Ns,[],Ns).
gt_hf(Ns,[e(X,Y)|Es],[X-Y|Hs]) :-
delete(Ns,X,Ns1),
delete(Ns1,Y,Ns2),
gt_hf(Ns2,Es,Hs).
% labelled digraph
ldt_hf(Ns,[],Ns).
ldt_hf(Ns,[a(X,Y,I)|As],[X>Y/I|Hs]) :-
delete(Ns,X,Ns1),
delete(Ns1,Y,Ns2),
ldt_hf(Ns2,As,Hs).
% unlabelled digraph
dt_hf(Ns,[],Ns).
dt_hf(Ns,[a(X,Y)|As],[X>Y|Hs]) :-
delete(Ns,X,Ns1),
delete(Ns1,Y,Ns2),
dt_hf(Ns2,As,Hs).
% we guess that if there is a '>' term then it's a digraph, else a graph
human_to_gterm(HF,digraph(Ns,As)) :- memberchk(_>_,HF), !,
hf_dt(HF,Ns1,As1), sort(Ns1,Ns), sort(As1,As).
human_to_gterm(HF,graph(Ns,Es)) :-
hf_gt(HF,Ns1,Es1), sort(Ns1,Ns), sort(Es1,Es).
% remember: sort/2 removes duplicates!
hf_gt([],[],[]).
hf_gt([X-Y/I|Hs],[X,Y|Ns],[e(U,V,I)|Es]) :- !,
sort0([X,Y],[U,V]), hf_gt(Hs,Ns,Es).
hf_gt([X-Y|Hs],[X,Y|Ns],[e(U,V)|Es]) :- !,
sort0([X,Y],[U,V]), hf_gt(Hs,Ns,Es).
hf_gt([H|Hs],[H|Ns],Es) :- hf_gt(Hs,Ns,Es).
hf_dt([],[],[]).
hf_dt([X>Y/I|Hs],[X,Y|Ns],[a(X,Y,I)|As]) :- !,
hf_dt(Hs,Ns,As).
hf_dt([X>Y|Hs],[X,Y|Ns],[a(X,Y)|As]) :- !,
hf_dt(Hs,Ns,As).
hf_dt([H|Hs],[H|Ns],As) :- hf_dt(Hs,Ns,As).
sort0([X,Y],[X,Y]) :- X @=< Y, !.
sort0([X,Y],[Y,X]) :- X @> Y.
%! \end{solution}?- human_gterm([b-c, f-c, g-h, d, f-b, k-f, h-g],G1), alist_gterm(Type,AL,G1).
Path
:- module(_, _, [assertions]).
:- use_module(library(idlists), [memberchk/2]).
:- use_module(library(sort)).
:- use_module(library(aggregates), [findall/3]).
:- use_module(library(classic/classic_predicates), [delete/3]).
:- data edge/2.
:- data arc/2.
:- test path(G,A,B,P) : (G = graph([b,c,d,f,g,h,k],[e(b,c),e(b,f),e(c,f),e(f,k),e(g,h)]), A = b, B = k) => (P = [b,f,k]; P = [b,c,f,k]) + (not_fails, num_solutions(2)).
sorry :- throw(not_solved_yet).
alist_gterm(Type,AL,GT):- nonvar(GT), !, gterm_to_alist(GT,Type,AL).
alist_gterm(Type,AL,GT):- atom(Type), nonvar(AL), alist_to_gterm(Type,AL,GT).
gterm_to_alist(graph(Ns,Es),graph,AL) :- memberchk(e(_,_,_),Es), ! ,
lgt_al(Ns,Es,AL).
gterm_to_alist(graph(Ns,Es),graph,AL) :- !,
gt_al(Ns,Es,AL).
gterm_to_alist(digraph(Ns,As),digraph,AL) :- memberchk(a(_,_,_),As), !,
ldt_al(Ns,As,AL).
gterm_to_alist(digraph(Ns,As),digraph,AL) :-
dt_al(Ns,As,AL).
lgt_al([],_,[]).
lgt_al([V|Vs],Es,[n(V,L)|Ns]) :-
findall(T,((member(e(X,V,I),Es) ; member(e(V,X,I),Es)),T = X/I),L),
lgt_al(Vs,Es,Ns).
gt_al([],_,[]).
gt_al([V|Vs],Es,[n(V,L)|Ns]) :-
findall(X,(member(e(X,V),Es) ; member(e(V,X),Es)),L), gt_al(Vs,Es,Ns).
ldt_al([],_,[]).
ldt_al([V|Vs],As,[n(V,L)|Ns]) :-
findall(T,(member(a(V,X,I),As), T=X/I),L), ldt_al(Vs,As,Ns).
dt_al([],_,[]).
dt_al([V|Vs],As,[n(V,L)|Ns]) :-
findall(X,member(a(V,X),As),L), dt_al(Vs,As,Ns).
alist_to_gterm(graph,AL,graph(Ns,Es)) :- !, al_gt(AL,Ns,EsU,[]), sort(EsU,Es).
alist_to_gterm(digraph,AL,digraph(Ns,As)) :- al_dt(AL,Ns,AsU,[]), sort(AsU,As).
al_gt([],[],Es,Es).
al_gt([n(V,Xs)|Ns],[V|Vs],Es,Acc) :-
add_edges(V,Xs,Acc1,Acc), al_gt(Ns,Vs,Es,Acc1).
add_edges(_,[],Es,Es).
add_edges(V,[X/_|Xs],Es,Acc) :- V @> X, !, add_edges(V,Xs,Es,Acc).
add_edges(V,[X|Xs],Es,Acc) :- V @> X, !, add_edges(V,Xs,Es,Acc).
add_edges(V,[X/I|Xs],Es,Acc) :- V @=< X, !, add_edges(V,Xs,Es,[e(V,X,I)|Acc]).
add_edges(V,[X|Xs],Es,Acc) :- V @=< X, add_edges(V,Xs,Es,[e(V,X)|Acc]).
al_dt([],[],As,As).
al_dt([n(V,Xs)|Ns],[V|Vs],As,Acc) :-
add_arcs(V,Xs,Acc1,Acc), al_dt(Ns,Vs,As,Acc1).
add_arcs(_,[],As,As).
add_arcs(V,[X/I|Xs],As,Acc) :- !, add_arcs(V,Xs,As,[a(V,X,I)|Acc]).
add_arcs(V,[X|Xs],As,Acc) :- add_arcs(V,Xs,As,[a(V,X)|Acc]).
ecl_to_gterm(GT) :-
findall(E,(edge(X,Y),E=X-Y),Es), human_gterm(Es,GT).
acl_to_gterm(GT) :-
findall(A,(arc(X,Y),A= >(X,Y)),As), human_gterm(As,GT).
human_gterm(HF,GT):- nonvar(GT), !, gterm_to_human(GT,HF).
human_gterm(HF,GT):- nonvar(HF), human_to_gterm(HF,GT).
gterm_to_human(graph(Ns,Es),HF) :- memberchk(e(_,_,_),Es), !,
lgt_hf(Ns,Es,HF).
gterm_to_human(graph(Ns,Es),HF) :- !,
gt_hf(Ns,Es,HF).
gterm_to_human(digraph(Ns,As),HF) :- memberchk(a(_,_,_),As), !,
ldt_hf(Ns,As,HF).
gterm_to_human(digraph(Ns,As),HF) :-
dt_hf(Ns,As,HF).
lgt_hf(Ns,[],Ns).
lgt_hf(Ns,[e(X,Y,I)|Es],[X-Y/I|Hs]) :-
delete(Ns,X,Ns1),
delete(Ns1,Y,Ns2),
lgt_hf(Ns2,Es,Hs).
gt_hf(Ns,[],Ns).
gt_hf(Ns,[e(X,Y)|Es],[X-Y|Hs]) :-
delete(Ns,X,Ns1),
delete(Ns1,Y,Ns2),
gt_hf(Ns2,Es,Hs).
ldt_hf(Ns,[],Ns).
ldt_hf(Ns,[a(X,Y,I)|As],[X>Y/I|Hs]) :-
delete(Ns,X,Ns1),
delete(Ns1,Y,Ns2),
ldt_hf(Ns2,As,Hs).
dt_hf(Ns,[],Ns).
dt_hf(Ns,[a(X,Y)|As],[X>Y|Hs]) :-
delete(Ns,X,Ns1),
delete(Ns1,Y,Ns2),
dt_hf(Ns2,As,Hs).
human_to_gterm(HF,digraph(Ns,As)) :- memberchk(_>_,HF), !,
hf_dt(HF,Ns1,As1), sort(Ns1,Ns), sort(As1,As).
human_to_gterm(HF,graph(Ns,Es)) :-
hf_gt(HF,Ns1,Es1), sort(Ns1,Ns), sort(Es1,Es).
hf_gt([],[],[]).
hf_gt([X-Y/I|Hs],[X,Y|Ns],[e(U,V,I)|Es]) :- !,
sort0([X,Y],[U,V]), hf_gt(Hs,Ns,Es).
hf_gt([X-Y|Hs],[X,Y|Ns],[e(U,V)|Es]) :- !,
sort0([X,Y],[U,V]), hf_gt(Hs,Ns,Es).
hf_gt([H|Hs],[H|Ns],Es) :- hf_gt(Hs,Ns,Es).
hf_dt([],[],[]).
hf_dt([X>Y/I|Hs],[X,Y|Ns],[a(X,Y,I)|As]) :- !,
hf_dt(Hs,Ns,As).
hf_dt([X>Y|Hs],[X,Y|Ns],[a(X,Y)|As]) :- !,
hf_dt(Hs,Ns,As).
hf_dt([H|Hs],[H|Ns],As) :- hf_dt(Hs,Ns,As).
sort0([X,Y],[X,Y]) :- X @=< Y, !.
sort0([X,Y],[Y,X]) :- X @> Y.
%! \begin{hint}
path(G,A,B,P) :- sorry.
% P is a (acyclic) path from node A to node B in the graph G.
% G is given in graph-term form.
% (+,+,+,?)
%! \end{hint}
%! \begin{solution}
path(G,A,B,P) :- path1(G,A,[B],P).
path1(_,A,[A|P1],[A|P1]).
path1(G,A,[Y|P1],P) :-
adjacent(X,Y,G), \+ memberchk(X,[Y|P1]), path1(G,A,[X,Y|P1],P).
% A useful predicate: adjacent/3
adjacent(X,Y,graph(_,Es)) :- member(e(X,Y),Es).
adjacent(X,Y,graph(_,Es)) :- member(e(Y,X),Es).
adjacent(X,Y,graph(_,Es)) :- member(e(X,Y,_),Es).
adjacent(X,Y,graph(_,Es)) :- member(e(Y,X,_),Es).
adjacent(X,Y,digraph(_,As)) :- member(a(X,Y),As).
adjacent(X,Y,digraph(_,As)) :- member(a(X,Y,_),As).
%! \end{solution}?- path(graph([b,c,d,f,g,h,k],[e(b,c),e(b,f),e(c,f),e(f,k),e(g,h)]),b,k,P).
Cycle
:- module(_, _, [assertions]).
:- use_module(library(idlists), [memberchk/2]).
:- use_module(library(sort)).
:- use_module(library(aggregates), [findall/3]).
:- use_module(library(classic/classic_predicates), [delete/3, append/3, length/2]).
:- data edge/2.
:- data arc/2.
:- test cycle(G,A,P) : (G = graph([b,c,d,f,g,h,k],[e(b,c),e(b,f),e(c,f),e(f,k),e(g,h)]), A = b) => (P = [b,f,c,b]; P = [b,c,f,b]) + (not_fails, num_solutions(2)).
sorry :- throw(not_solved_yet).
alist_gterm(Type,AL,GT):- nonvar(GT), !, gterm_to_alist(GT,Type,AL).
alist_gterm(Type,AL,GT):- atom(Type), nonvar(AL), alist_to_gterm(Type,AL,GT).
gterm_to_alist(graph(Ns,Es),graph,AL) :- memberchk(e(_,_,_),Es), ! ,
lgt_al(Ns,Es,AL).
gterm_to_alist(graph(Ns,Es),graph,AL) :- !,
gt_al(Ns,Es,AL).
gterm_to_alist(digraph(Ns,As),digraph,AL) :- memberchk(a(_,_,_),As), !,
ldt_al(Ns,As,AL).
gterm_to_alist(digraph(Ns,As),digraph,AL) :-
dt_al(Ns,As,AL).
lgt_al([],_,[]).
lgt_al([V|Vs],Es,[n(V,L)|Ns]) :-
findall(T,((member(e(X,V,I),Es) ; member(e(V,X,I),Es)),T = X/I),L),
lgt_al(Vs,Es,Ns).
gt_al([],_,[]).
gt_al([V|Vs],Es,[n(V,L)|Ns]) :-
findall(X,(member(e(X,V),Es) ; member(e(V,X),Es)),L), gt_al(Vs,Es,Ns).
ldt_al([],_,[]).
ldt_al([V|Vs],As,[n(V,L)|Ns]) :-
findall(T,(member(a(V,X,I),As), T=X/I),L), ldt_al(Vs,As,Ns).
dt_al([],_,[]).
dt_al([V|Vs],As,[n(V,L)|Ns]) :-
findall(X,member(a(V,X),As),L), dt_al(Vs,As,Ns).
alist_to_gterm(graph,AL,graph(Ns,Es)) :- !, al_gt(AL,Ns,EsU,[]), sort(EsU,Es).
alist_to_gterm(digraph,AL,digraph(Ns,As)) :- al_dt(AL,Ns,AsU,[]), sort(AsU,As).
al_gt([],[],Es,Es).
al_gt([n(V,Xs)|Ns],[V|Vs],Es,Acc) :-
add_edges(V,Xs,Acc1,Acc), al_gt(Ns,Vs,Es,Acc1).
add_edges(_,[],Es,Es).
add_edges(V,[X/_|Xs],Es,Acc) :- V @> X, !, add_edges(V,Xs,Es,Acc).
add_edges(V,[X|Xs],Es,Acc) :- V @> X, !, add_edges(V,Xs,Es,Acc).
add_edges(V,[X/I|Xs],Es,Acc) :- V @=< X, !, add_edges(V,Xs,Es,[e(V,X,I)|Acc]).
add_edges(V,[X|Xs],Es,Acc) :- V @=< X, add_edges(V,Xs,Es,[e(V,X)|Acc]).
al_dt([],[],As,As).
al_dt([n(V,Xs)|Ns],[V|Vs],As,Acc) :-
add_arcs(V,Xs,Acc1,Acc), al_dt(Ns,Vs,As,Acc1).
add_arcs(_,[],As,As).
add_arcs(V,[X/I|Xs],As,Acc) :- !, add_arcs(V,Xs,As,[a(V,X,I)|Acc]).
add_arcs(V,[X|Xs],As,Acc) :- add_arcs(V,Xs,As,[a(V,X)|Acc]).
ecl_to_gterm(GT) :-
findall(E,(edge(X,Y),E=X-Y),Es), human_gterm(Es,GT).
acl_to_gterm(GT) :-
findall(A,(arc(X,Y),A= >(X,Y)),As), human_gterm(As,GT).
human_gterm(HF,GT):- nonvar(GT), !, gterm_to_human(GT,HF).
human_gterm(HF,GT):- nonvar(HF), human_to_gterm(HF,GT).
gterm_to_human(graph(Ns,Es),HF) :- memberchk(e(_,_,_),Es), !,
lgt_hf(Ns,Es,HF).
gterm_to_human(graph(Ns,Es),HF) :- !,
gt_hf(Ns,Es,HF).
gterm_to_human(digraph(Ns,As),HF) :- memberchk(a(_,_,_),As), !,
ldt_hf(Ns,As,HF).
gterm_to_human(digraph(Ns,As),HF) :-
dt_hf(Ns,As,HF).
lgt_hf(Ns,[],Ns).
lgt_hf(Ns,[e(X,Y,I)|Es],[X-Y/I|Hs]) :-
delete(Ns,X,Ns1),
delete(Ns1,Y,Ns2),
lgt_hf(Ns2,Es,Hs).
gt_hf(Ns,[],Ns).
gt_hf(Ns,[e(X,Y)|Es],[X-Y|Hs]) :-
delete(Ns,X,Ns1),
delete(Ns1,Y,Ns2),
gt_hf(Ns2,Es,Hs).
ldt_hf(Ns,[],Ns).
ldt_hf(Ns,[a(X,Y,I)|As],[X>Y/I|Hs]) :-
delete(Ns,X,Ns1),
delete(Ns1,Y,Ns2),
ldt_hf(Ns2,As,Hs).
dt_hf(Ns,[],Ns).
dt_hf(Ns,[a(X,Y)|As],[X>Y|Hs]) :-
delete(Ns,X,Ns1),
delete(Ns1,Y,Ns2),
dt_hf(Ns2,As,Hs).
human_to_gterm(HF,digraph(Ns,As)) :- memberchk(_>_,HF), !,
hf_dt(HF,Ns1,As1), sort(Ns1,Ns), sort(As1,As).
human_to_gterm(HF,graph(Ns,Es)) :-
hf_gt(HF,Ns1,Es1), sort(Ns1,Ns), sort(Es1,Es).
hf_gt([],[],[]).
hf_gt([X-Y/I|Hs],[X,Y|Ns],[e(U,V,I)|Es]) :- !,
sort0([X,Y],[U,V]), hf_gt(Hs,Ns,Es).
hf_gt([X-Y|Hs],[X,Y|Ns],[e(U,V)|Es]) :- !,
sort0([X,Y],[U,V]), hf_gt(Hs,Ns,Es).
hf_gt([H|Hs],[H|Ns],Es) :- hf_gt(Hs,Ns,Es).
hf_dt([],[],[]).
hf_dt([X>Y/I|Hs],[X,Y|Ns],[a(X,Y,I)|As]) :- !,
hf_dt(Hs,Ns,As).
hf_dt([X>Y|Hs],[X,Y|Ns],[a(X,Y)|As]) :- !,
hf_dt(Hs,Ns,As).
hf_dt([H|Hs],[H|Ns],As) :- hf_dt(Hs,Ns,As).
sort0([X,Y],[X,Y]) :- X @=< Y, !.
sort0([X,Y],[Y,X]) :- X @> Y.
path(G,A,B,P) :- path1(G,A,[B],P).
path1(_,A,[A|P1],[A|P1]).
path1(G,A,[Y|P1],P) :-
adjacent(X,Y,G), \+ memberchk(X,[Y|P1]), path1(G,A,[X,Y|P1],P).
adjacent(X,Y,graph(_,Es)) :- member(e(X,Y),Es).
adjacent(X,Y,graph(_,Es)) :- member(e(Y,X),Es).
adjacent(X,Y,graph(_,Es)) :- member(e(X,Y,_),Es).
adjacent(X,Y,graph(_,Es)) :- member(e(Y,X,_),Es).
adjacent(X,Y,digraph(_,As)) :- member(a(X,Y),As).
adjacent(X,Y,digraph(_,As)) :- member(a(X,Y,_),As).
%! \begin{hint}
cycle(G,A,P) :- sorry.
% P is a closed path starting at node A in the graph G.
% G is given in graph-term form.
% (+,+,?)
%! \end{hint}
%! \begin{solution}
cycle(G,A,P) :-
adjacent(B,A,G), path(G,A,B,P1), length(P1,L), L > 2, append(P1,[A],P).
%! \end{solution}?- cycle(graph([b,c,d,f,g,h,k],[e(b,c),e(b,f),e(c,f),e(f,k),e(g,h)]),b,P).
Spanning trees
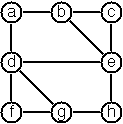
:- module(_, _, [assertions]).
:- use_module(library(idlists), [memberchk/2]).
:- use_module(library(sort)).
:- use_module(library(aggregates), [findall/3]).
:- use_module(library(classic/classic_predicates), [delete/3, select/3]).
:- data edge/2.
:- data arc/2.
sorry :- throw(not_solved_yet).
:- test is_connected(A) : (A = graph([a,b,c,d,e,f,g,h],[e(a,b),e(a,d),e(b,c),e(b,e),e(c,e),e(e,d),e(d,f),e(e,h),e(d,g),e(f,g), e(g,h)])) + (not_fails).
:- test is_tree(A) : (A = graph([a,b,c,d,e,f,g,h],[e(a,b),e(a,d),e(b,c),e(b,e),e(c,e),e(e,d),e(d,f),e(e,h),e(d,g),e(f,g), e(g,h)])) + (fails).
alist_gterm(Type,AL,GT):- nonvar(GT), !, gterm_to_alist(GT,Type,AL).
alist_gterm(Type,AL,GT):- atom(Type), nonvar(AL), alist_to_gterm(Type,AL,GT).
gterm_to_alist(graph(Ns,Es),graph,AL) :- memberchk(e(_,_,_),Es), ! ,
lgt_al(Ns,Es,AL).
gterm_to_alist(graph(Ns,Es),graph,AL) :- !,
gt_al(Ns,Es,AL).
gterm_to_alist(digraph(Ns,As),digraph,AL) :- memberchk(a(_,_,_),As), !,
ldt_al(Ns,As,AL).
gterm_to_alist(digraph(Ns,As),digraph,AL) :-
dt_al(Ns,As,AL).
lgt_al([],_,[]).
lgt_al([V|Vs],Es,[n(V,L)|Ns]) :-
findall(T,((member(e(X,V,I),Es) ; member(e(V,X,I),Es)),T = X/I),L),
lgt_al(Vs,Es,Ns).
gt_al([],_,[]).
gt_al([V|Vs],Es,[n(V,L)|Ns]) :-
findall(X,(member(e(X,V),Es) ; member(e(V,X),Es)),L), gt_al(Vs,Es,Ns).
ldt_al([],_,[]).
ldt_al([V|Vs],As,[n(V,L)|Ns]) :-
findall(T,(member(a(V,X,I),As), T=X/I),L), ldt_al(Vs,As,Ns).
dt_al([],_,[]).
dt_al([V|Vs],As,[n(V,L)|Ns]) :-
findall(X,member(a(V,X),As),L), dt_al(Vs,As,Ns).
alist_to_gterm(graph,AL,graph(Ns,Es)) :- !, al_gt(AL,Ns,EsU,[]), sort(EsU,Es).
alist_to_gterm(digraph,AL,digraph(Ns,As)) :- al_dt(AL,Ns,AsU,[]), sort(AsU,As).
al_gt([],[],Es,Es).
al_gt([n(V,Xs)|Ns],[V|Vs],Es,Acc) :-
add_edges(V,Xs,Acc1,Acc), al_gt(Ns,Vs,Es,Acc1).
add_edges(_,[],Es,Es).
add_edges(V,[X/_|Xs],Es,Acc) :- V @> X, !, add_edges(V,Xs,Es,Acc).
add_edges(V,[X|Xs],Es,Acc) :- V @> X, !, add_edges(V,Xs,Es,Acc).
add_edges(V,[X/I|Xs],Es,Acc) :- V @=< X, !, add_edges(V,Xs,Es,[e(V,X,I)|Acc]).
add_edges(V,[X|Xs],Es,Acc) :- V @=< X, add_edges(V,Xs,Es,[e(V,X)|Acc]).
al_dt([],[],As,As).
al_dt([n(V,Xs)|Ns],[V|Vs],As,Acc) :-
add_arcs(V,Xs,Acc1,Acc), al_dt(Ns,Vs,As,Acc1).
add_arcs(_,[],As,As).
add_arcs(V,[X/I|Xs],As,Acc) :- !, add_arcs(V,Xs,As,[a(V,X,I)|Acc]).
add_arcs(V,[X|Xs],As,Acc) :- add_arcs(V,Xs,As,[a(V,X)|Acc]).
ecl_to_gterm(GT) :-
findall(E,(edge(X,Y),E=X-Y),Es), human_gterm(Es,GT).
acl_to_gterm(GT) :-
findall(A,(arc(X,Y),A= >(X,Y)),As), human_gterm(As,GT).
human_gterm(HF,GT):- nonvar(GT), !, gterm_to_human(GT,HF).
human_gterm(HF,GT):- nonvar(HF), human_to_gterm(HF,GT).
gterm_to_human(graph(Ns,Es),HF) :- memberchk(e(_,_,_),Es), !,
lgt_hf(Ns,Es,HF).
gterm_to_human(graph(Ns,Es),HF) :- !,
gt_hf(Ns,Es,HF).
gterm_to_human(digraph(Ns,As),HF) :- memberchk(a(_,_,_),As), !,
ldt_hf(Ns,As,HF).
gterm_to_human(digraph(Ns,As),HF) :-
dt_hf(Ns,As,HF).
lgt_hf(Ns,[],Ns).
lgt_hf(Ns,[e(X,Y,I)|Es],[X-Y/I|Hs]) :-
delete(Ns,X,Ns1),
delete(Ns1,Y,Ns2),
lgt_hf(Ns2,Es,Hs).
gt_hf(Ns,[],Ns).
gt_hf(Ns,[e(X,Y)|Es],[X-Y|Hs]) :-
delete(Ns,X,Ns1),
delete(Ns1,Y,Ns2),
gt_hf(Ns2,Es,Hs).
ldt_hf(Ns,[],Ns).
ldt_hf(Ns,[a(X,Y,I)|As],[X>Y/I|Hs]) :-
delete(Ns,X,Ns1),
delete(Ns1,Y,Ns2),
ldt_hf(Ns2,As,Hs).
dt_hf(Ns,[],Ns).
dt_hf(Ns,[a(X,Y)|As],[X>Y|Hs]) :-
delete(Ns,X,Ns1),
delete(Ns1,Y,Ns2),
dt_hf(Ns2,As,Hs).
human_to_gterm(HF,digraph(Ns,As)) :- memberchk(_>_,HF), !,
hf_dt(HF,Ns1,As1), sort(Ns1,Ns), sort(As1,As).
human_to_gterm(HF,graph(Ns,Es)) :-
hf_gt(HF,Ns1,Es1), sort(Ns1,Ns), sort(Es1,Es).
hf_gt([],[],[]).
hf_gt([X-Y/I|Hs],[X,Y|Ns],[e(U,V,I)|Es]) :- !,
sort0([X,Y],[U,V]), hf_gt(Hs,Ns,Es).
hf_gt([X-Y|Hs],[X,Y|Ns],[e(U,V)|Es]) :- !,
sort0([X,Y],[U,V]), hf_gt(Hs,Ns,Es).
hf_gt([H|Hs],[H|Ns],Es) :- hf_gt(Hs,Ns,Es).
hf_dt([],[],[]).
hf_dt([X>Y/I|Hs],[X,Y|Ns],[a(X,Y,I)|As]) :- !,
hf_dt(Hs,Ns,As).
hf_dt([X>Y|Hs],[X,Y|Ns],[a(X,Y)|As]) :- !,
hf_dt(Hs,Ns,As).
hf_dt([H|Hs],[H|Ns],As) :- hf_dt(Hs,Ns,As).
sort0([X,Y],[X,Y]) :- X @=< Y, !.
sort0([X,Y],[Y,X]) :- X @> Y.
%! \begin{hint}
s_tree(G,T) :- sorry.
% T is a spanning tree of the graph G
% (graph-term graph-term) (+,?)
transfer(Ns,GEs,TEs) :- sorry.
% transfer edges from GEs (graph edges)
% to TEs (tree edges) until the list NS of still unconnected tree nodes
% becomes empty. An edge is accepted if and only if one end-point is
% already connected to the tree and the other is not.
% Another use is the following connectivity tester:
is_tree(G) :- sorry.
% the graph G is a tree
is_connected(G) :- sorry.
% the graph G is connected
%! \end{hint}
%! \begin{solution}
s_tree(graph([N|Ns],GraphEdges),graph([N|Ns],TreeEdges)) :-
transfer(Ns,GraphEdges,TreeEdgesUnsorted),
sort(TreeEdgesUnsorted,TreeEdges).
transfer([],_,[]).
transfer(Ns,GEs,[GE|TEs]) :-
select(GE,GEs,GEs1),
incident(GE,X,Y),
acceptable(X,Y,Ns),
delete(Ns,X,Ns1),
delete(Ns1,Y,Ns2),
transfer(Ns2,GEs1,TEs).
incident(e(X,Y),X,Y).
incident(e(X,Y,_),X,Y).
acceptable(X,Y,Ns) :- memberchk(X,Ns), \+ memberchk(Y,Ns), !.
acceptable(X,Y,Ns) :- memberchk(Y,Ns), \+ memberchk(X,Ns).
% An almost trivial use of the predicate s_tree/2 is the following
% tree tester predicate:
% is_tree(G) :- the graph G is a tree
is_tree(G) :- s_tree(G,G), !.
% is_connected(G) :- the graph G is connected
is_connected(G) :- s_tree(G,_), !.
%! \end{solution}?- is_connected(graph([a,b,c,d,e,f,g,h],[e(a,b),e(a,d),e(b,c),e(b,e),e(c,e),e(e,d),e(d,f),e(e,h),e(d,g),e(f,g), e(g,h)])).
?- is_tree(graph([a,b,c,d,e,f,g,h],[e(a,b),e(a,d),e(b,c),e(b,e),e(c,e),e(d,e),e(d,f),e(d,g),e(e,h),e(f,g),e(g,h)])).
Node degree and graph coloration
a) Write a predicate degree(Graph,Node,Deg) that determines the degree of a given node.
b) Write a predicate that generates a list of all nodes of a graph sorted according to decreasing degree.
c) Use Welch-Powell's algorithm to paint the nodes of a graph in such a way that adjacent nodes have different colors.
:- module(_, _, [assertions]).
:- push_prolog_flag(multi_arity_warnings, off).
:- use_module(library(idlists), [memberchk/2]).
:- use_module(library(sort)).
:- use_module(library(aggregates), [findall/3]).
:- use_module(library(classic/classic_predicates), [delete/3, length/2]).
:- data edge/2.
:- data arc/2.
sorry :- throw(not_solved_yet).
alist_gterm(Type,AL,GT):- nonvar(GT), !, gterm_to_alist(GT,Type,AL).
alist_gterm(Type,AL,GT):- atom(Type), nonvar(AL), alist_to_gterm(Type,AL,GT).
gterm_to_alist(graph(Ns,Es),graph,AL) :- memberchk(e(_,_,_),Es), ! ,
lgt_al(Ns,Es,AL).
gterm_to_alist(graph(Ns,Es),graph,AL) :- !,
gt_al(Ns,Es,AL).
gterm_to_alist(digraph(Ns,As),digraph,AL) :- memberchk(a(_,_,_),As), !,
ldt_al(Ns,As,AL).
gterm_to_alist(digraph(Ns,As),digraph,AL) :-
dt_al(Ns,As,AL).
lgt_al([],_,[]).
lgt_al([V|Vs],Es,[n(V,L)|Ns]) :-
findall(T,((member(e(X,V,I),Es) ; member(e(V,X,I),Es)),T = X/I),L),
lgt_al(Vs,Es,Ns).
gt_al([],_,[]).
gt_al([V|Vs],Es,[n(V,L)|Ns]) :-
findall(X,(member(e(X,V),Es) ; member(e(V,X),Es)),L), gt_al(Vs,Es,Ns).
ldt_al([],_,[]).
ldt_al([V|Vs],As,[n(V,L)|Ns]) :-
findall(T,(member(a(V,X,I),As), T=X/I),L), ldt_al(Vs,As,Ns).
dt_al([],_,[]).
dt_al([V|Vs],As,[n(V,L)|Ns]) :-
findall(X,member(a(V,X),As),L), dt_al(Vs,As,Ns).
alist_to_gterm(graph,AL,graph(Ns,Es)) :- !, al_gt(AL,Ns,EsU,[]), sort(EsU,Es).
alist_to_gterm(digraph,AL,digraph(Ns,As)) :- al_dt(AL,Ns,AsU,[]), sort(AsU,As).
al_gt([],[],Es,Es).
al_gt([n(V,Xs)|Ns],[V|Vs],Es,Acc) :-
add_edges(V,Xs,Acc1,Acc), al_gt(Ns,Vs,Es,Acc1).
add_edges(_,[],Es,Es).
add_edges(V,[X/_|Xs],Es,Acc) :- V @> X, !, add_edges(V,Xs,Es,Acc).
add_edges(V,[X|Xs],Es,Acc) :- V @> X, !, add_edges(V,Xs,Es,Acc).
add_edges(V,[X/I|Xs],Es,Acc) :- V @=< X, !, add_edges(V,Xs,Es,[e(V,X,I)|Acc]).
add_edges(V,[X|Xs],Es,Acc) :- V @=< X, add_edges(V,Xs,Es,[e(V,X)|Acc]).
al_dt([],[],As,As).
al_dt([n(V,Xs)|Ns],[V|Vs],As,Acc) :-
add_arcs(V,Xs,Acc1,Acc), al_dt(Ns,Vs,As,Acc1).
add_arcs(_,[],As,As).
add_arcs(V,[X/I|Xs],As,Acc) :- !, add_arcs(V,Xs,As,[a(V,X,I)|Acc]).
add_arcs(V,[X|Xs],As,Acc) :- add_arcs(V,Xs,As,[a(V,X)|Acc]).
ecl_to_gterm(GT) :-
findall(E,(edge(X,Y),E=X-Y),Es), human_gterm(Es,GT).
acl_to_gterm(GT) :-
findall(A,(arc(X,Y),A= >(X,Y)),As), human_gterm(As,GT).
human_gterm(HF,GT):- nonvar(GT), !, gterm_to_human(GT,HF).
human_gterm(HF,GT):- nonvar(HF), human_to_gterm(HF,GT).
gterm_to_human(graph(Ns,Es),HF) :- memberchk(e(_,_,_),Es), !,
lgt_hf(Ns,Es,HF).
gterm_to_human(graph(Ns,Es),HF) :- !,
gt_hf(Ns,Es,HF).
gterm_to_human(digraph(Ns,As),HF) :- memberchk(a(_,_,_),As), !,
ldt_hf(Ns,As,HF).
gterm_to_human(digraph(Ns,As),HF) :-
dt_hf(Ns,As,HF).
lgt_hf(Ns,[],Ns).
lgt_hf(Ns,[e(X,Y,I)|Es],[X-Y/I|Hs]) :-
delete(Ns,X,Ns1),
delete(Ns1,Y,Ns2),
lgt_hf(Ns2,Es,Hs).
gt_hf(Ns,[],Ns).
gt_hf(Ns,[e(X,Y)|Es],[X-Y|Hs]) :-
delete(Ns,X,Ns1),
delete(Ns1,Y,Ns2),
gt_hf(Ns2,Es,Hs).
ldt_hf(Ns,[],Ns).
ldt_hf(Ns,[a(X,Y,I)|As],[X>Y/I|Hs]) :-
delete(Ns,X,Ns1),
delete(Ns1,Y,Ns2),
ldt_hf(Ns2,As,Hs).
dt_hf(Ns,[],Ns).
dt_hf(Ns,[a(X,Y)|As],[X>Y|Hs]) :-
delete(Ns,X,Ns1),
delete(Ns1,Y,Ns2),
dt_hf(Ns2,As,Hs).
human_to_gterm(HF,digraph(Ns,As)) :- memberchk(_>_,HF), !,
hf_dt(HF,Ns1,As1), sort(Ns1,Ns), sort(As1,As).
human_to_gterm(HF,graph(Ns,Es)) :-
hf_gt(HF,Ns1,Es1), sort(Ns1,Ns), sort(Es1,Es).
hf_gt([],[],[]).
hf_gt([X-Y/I|Hs],[X,Y|Ns],[e(U,V,I)|Es]) :- !,
sort0([X,Y],[U,V]), hf_gt(Hs,Ns,Es).
hf_gt([X-Y|Hs],[X,Y|Ns],[e(U,V)|Es]) :- !,
sort0([X,Y],[U,V]), hf_gt(Hs,Ns,Es).
hf_gt([H|Hs],[H|Ns],Es) :- hf_gt(Hs,Ns,Es).
hf_dt([],[],[]).
hf_dt([X>Y/I|Hs],[X,Y|Ns],[a(X,Y,I)|As]) :- !,
hf_dt(Hs,Ns,As).
hf_dt([X>Y|Hs],[X,Y|Ns],[a(X,Y)|As]) :- !,
hf_dt(Hs,Ns,As).
hf_dt([H|Hs],[H|Ns],As) :- hf_dt(Hs,Ns,As).
sort0([X,Y],[X,Y]) :- X @=< Y, !.
sort0([X,Y],[Y,X]) :- X @> Y.
path(G,A,B,P) :- path1(G,A,[B],P).
path1(_,A,[A|P1],[A|P1]).
path1(G,A,[Y|P1],P) :-
adjacent(X,Y,G), \+ memberchk(X,[Y|P1]), path1(G,A,[X,Y|P1],P).
adjacent(X,Y,graph(_,Es)) :- member(e(X,Y),Es).
adjacent(X,Y,graph(_,Es)) :- member(e(Y,X),Es).
adjacent(X,Y,graph(_,Es)) :- member(e(X,Y,_),Es).
adjacent(X,Y,graph(_,Es)) :- member(e(Y,X,_),Es).
adjacent(X,Y,digraph(_,As)) :- member(a(X,Y),As).
adjacent(X,Y,digraph(_,As)) :- member(a(X,Y,_),As).
%! \begin{hint}
% a) Write a predicate degree(Graph,Node,Deg) that determines the degree
% of a given node.
degree(Graph,Node,Deg) :- sorry.
% Deg is the degree of the node Node in the graph Graph.
% (graph-term, node, integer), (+,+,?).
% --------------------------------------------------------------------------
% b) Write a predicate that generates a list of all nodes of a graph
% sorted according to decreasing degree.
degree_sorted_nodes(Graph,Nodes) :- sorry.
% Nodes is the list of the nodes
% of the graph Graph, sorted according to decreasing degree.
% --------------------------------------------------------------------------
% c) Use Welch-Powell's algorithm to paint the nodes of a graph in such
% a way that adjacent nodes have different colors.
% Use Welch-Powell's algorithm to paint the nodes of a graph
% in such a way that adjacent nodes have different colors.
paint(Graph,ColoredNodes) :- sorry.
paint_nodes(Graph,Ns,AccNodes,Color,ColoNodes) :- sorry.
% paint the remaining nodes Ns with a color number Color or higher.
% AccNodes is the set of nodes already colored. Return the result in ColoNodes.
% (graph-term,node-list,c-node-list,integer,c-node-list)
% (+,+,+,+,-)
paint_nodes(Graph,DSNs,Ns,AccNodes,Color,ColoNodes) :- sorry.
% paint the nodes in Ns with a fixed color number Color, if possible.
% If Ns is empty, continue with the next color number.
% AccNodes is the set of nodes already colored. Return the result in ColoNodes.
% (graph-term,node-list,c-node-list,c-node-list,integer,c-node-list)
% (+,+,+,+,+,-)
%! \end{hint}
%! \begin{solution}
% a) Write a predicate degree(Graph,Node,Deg) that determines the degree
% of a given node.
degree(graph(Ns,Es),Node,Deg) :-
alist_gterm(graph,AList,graph(Ns,Es)),
member(n(Node,AdjList),AList), !,
length(AdjList,Deg).
% --------------------------------------------------------------------------
% b) Write a predicate that generates a list of all nodes of a graph
% sorted according to decreasing degree.
% degree_sorted_nodes(Graph,Nodes) :- Nodes is the list of the nodes
% of the graph Graph, sorted according to decreasing degree.
degree_sorted_nodes(graph(Ns,Es),DSNodes) :-
alist_gterm(graph,AList,graph(Ns,Es)),
predsort(compare_degree,AList,AListDegreeSorted),
reduce(AListDegreeSorted,DSNodes).
compare_degree(Order,n(N1,AL1),n(N2,AL2)) :-
length(AL1,D1), length(AL2,D2),
compare(Order,D2+N1,D1+N2).
% Note: compare(Order,D2+N1,D1+N2) sorts the nodes according to
% decreasing degree, but alphabetically if the degrees are equal. Cool!
reduce([],[]).
reduce([n(N,_)|Ns],[N|NsR]) :- reduce(Ns,NsR).
% --------------------------------------------------------------------------
% c) Use Welch-Powell's algorithm to paint the nodes of a graph in such
% a way that adjacent nodes have different colors.
% Use Welch-Powell's algorithm to paint the nodes of a graph
% in such a way that adjacent nodes have different colors.
paint(Graph,ColoredNodes) :-
degree_sorted_nodes(Graph,DSNs),
paint_nodes(Graph,DSNs,[],1,ColoredNodes).
% paint_nodes(Graph,Ns,AccNodes,Color,ColoNodes) :- paint the remaining
% nodes Ns with a color number Color or higher. AccNodes is the set
% of nodes already colored. Return the result in ColoNodes.
% (graph-term,node-list,c-node-list,integer,c-node-list)
% (+,+,+,+,-)
paint_nodes(_,[],ColoNodes,_,ColoNodes) :- !.
paint_nodes(Graph,Ns,AccNodes,Color,ColoNodes) :-
paint_nodes(Graph,Ns,Ns,AccNodes,Color,ColoNodes).
% paint_nodes(Graph,DSNs,Ns,AccNodes,Color,ColoNodes) :- paint the
% nodes in Ns with a fixed color number Color, if possible.
% If Ns is empty, continue with the next color number.
% AccNodes is the set of nodes already colored.
% Return the result in ColoNodes.
% (graph-term,node-list,c-node-list,c-node-list,integer,c-node-list)
% (+,+,+,+,+,-)
paint_nodes(Graph,Ns,[],AccNodes,Color,ColoNodes) :- !,
Color1 is Color+1,
paint_nodes(Graph,Ns,AccNodes,Color1,ColoNodes).
paint_nodes(Graph,DSNs,[N|Ns],AccNodes,Color,ColoNodes) :-
\+ has_neighbor(Graph,N,Color,AccNodes), !,
delete(DSNs,N,DSNs1),
paint_nodes(Graph,DSNs1,Ns,[c(N,Color)|AccNodes],Color,ColoNodes).
paint_nodes(Graph,DSNs,[_|Ns],AccNodes,Color,ColoNodes) :-
paint_nodes(Graph,DSNs,Ns,AccNodes,Color,ColoNodes).
has_neighbor(Graph,N,Color,AccNodes) :-
adjacent(N,X,Graph),
memberchk(c(X,Color),AccNodes).
%! \end{solution}?- degree(graph([a,b,c,d,e,f,g,h],[e(a,b,5),e(a,d,3),e(b,c,2),e(b,e,4),e(c,e,6),e(e,d,7),e(d,f,4),e(e,h,3),e(d,g,5),e(f,g,4),e(g,h,1)]),b,A).
:- module(_, _, [assertions, datafacts]).
:- push_prolog_flag(multi_arity_warnings, off).
:- use_module(library(idlists), [memberchk/2]).
:- use_module(library(sort)).
:- use_module(library(aggregates), [findall/3, bagof/3]).
:- use_module(library(classic/classic_predicates), [delete/3, recorded/3, recorda/3, recordz/3]).
:- data edge/2.
:- data arc/2.
:- test depth_first_order(A,B,C) : (A = graph([a,b,c,d,e,f,g,h],[e(a,e),e(a,b),e(a,d),e(b,c),e(b,e),e(c,e),e(e,d),e(d,f),e(g,h)]), B = h) => (C = [g]; C = [h]) + (not_fails, num_solutions(2)).
sorry :- throw(not_solved_yet).
:- test depth_first_order(A,B,C) : (A = graph([h],[e(h,h)]), B = h) => (C = [h]) + (not_fails, is_det).
sorry :- throw(not_solved_yet).
alist_gterm(Type,AL,GT):- nonvar(GT), !, gterm_to_alist(GT,Type,AL).
alist_gterm(Type,AL,GT):- atom(Type), nonvar(AL), alist_to_gterm(Type,AL,GT).
gterm_to_alist(graph(Ns,Es),graph,AL) :- memberchk(e(_,_,_),Es), ! ,
lgt_al(Ns,Es,AL).
gterm_to_alist(graph(Ns,Es),graph,AL) :- !,
gt_al(Ns,Es,AL).
gterm_to_alist(digraph(Ns,As),digraph,AL) :- memberchk(a(_,_,_),As), !,
ldt_al(Ns,As,AL).
gterm_to_alist(digraph(Ns,As),digraph,AL) :-
dt_al(Ns,As,AL).
lgt_al([],_,[]).
lgt_al([V|Vs],Es,[n(V,L)|Ns]) :-
findall(T,((member(e(X,V,I),Es) ; member(e(V,X,I),Es)),T = X/I),L),
lgt_al(Vs,Es,Ns).
gt_al([],_,[]).
gt_al([V|Vs],Es,[n(V,L)|Ns]) :-
findall(X,(member(e(X,V),Es) ; member(e(V,X),Es)),L), gt_al(Vs,Es,Ns).
ldt_al([],_,[]).
ldt_al([V|Vs],As,[n(V,L)|Ns]) :-
findall(T,(member(a(V,X,I),As), T=X/I),L), ldt_al(Vs,As,Ns).
dt_al([],_,[]).
dt_al([V|Vs],As,[n(V,L)|Ns]) :-
findall(X,member(a(V,X),As),L), dt_al(Vs,As,Ns).
alist_to_gterm(graph,AL,graph(Ns,Es)) :- !, al_gt(AL,Ns,EsU,[]), sort(EsU,Es).
alist_to_gterm(digraph,AL,digraph(Ns,As)) :- al_dt(AL,Ns,AsU,[]), sort(AsU,As).
al_gt([],[],Es,Es).
al_gt([n(V,Xs)|Ns],[V|Vs],Es,Acc) :-
add_edges(V,Xs,Acc1,Acc), al_gt(Ns,Vs,Es,Acc1).
add_edges(_,[],Es,Es).
add_edges(V,[X/_|Xs],Es,Acc) :- V @> X, !, add_edges(V,Xs,Es,Acc).
add_edges(V,[X|Xs],Es,Acc) :- V @> X, !, add_edges(V,Xs,Es,Acc).
add_edges(V,[X/I|Xs],Es,Acc) :- V @=< X, !, add_edges(V,Xs,Es,[e(V,X,I)|Acc]).
add_edges(V,[X|Xs],Es,Acc) :- V @=< X, add_edges(V,Xs,Es,[e(V,X)|Acc]).
al_dt([],[],As,As).
al_dt([n(V,Xs)|Ns],[V|Vs],As,Acc) :-
add_arcs(V,Xs,Acc1,Acc), al_dt(Ns,Vs,As,Acc1).
add_arcs(_,[],As,As).
add_arcs(V,[X/I|Xs],As,Acc) :- !, add_arcs(V,Xs,As,[a(V,X,I)|Acc]).
add_arcs(V,[X|Xs],As,Acc) :- add_arcs(V,Xs,As,[a(V,X)|Acc]).
ecl_to_gterm(GT) :-
findall(E,(edge(X,Y),E=X-Y),Es), human_gterm(Es,GT).
acl_to_gterm(GT) :-
findall(A,(arc(X,Y),A= >(X,Y)),As), human_gterm(As,GT).
human_gterm(HF,GT):- nonvar(GT), !, gterm_to_human(GT,HF).
human_gterm(HF,GT):- nonvar(HF), human_to_gterm(HF,GT).
gterm_to_human(graph(Ns,Es),HF) :- memberchk(e(_,_,_),Es), !,
lgt_hf(Ns,Es,HF).
gterm_to_human(graph(Ns,Es),HF) :- !,
gt_hf(Ns,Es,HF).
gterm_to_human(digraph(Ns,As),HF) :- memberchk(a(_,_,_),As), !,
ldt_hf(Ns,As,HF).
gterm_to_human(digraph(Ns,As),HF) :-
dt_hf(Ns,As,HF).
lgt_hf(Ns,[],Ns).
lgt_hf(Ns,[e(X,Y,I)|Es],[X-Y/I|Hs]) :-
delete(Ns,X,Ns1),
delete(Ns1,Y,Ns2),
lgt_hf(Ns2,Es,Hs).
gt_hf(Ns,[],Ns).
gt_hf(Ns,[e(X,Y)|Es],[X-Y|Hs]) :-
delete(Ns,X,Ns1),
delete(Ns1,Y,Ns2),
gt_hf(Ns2,Es,Hs).
ldt_hf(Ns,[],Ns).
ldt_hf(Ns,[a(X,Y,I)|As],[X>Y/I|Hs]) :-
delete(Ns,X,Ns1),
delete(Ns1,Y,Ns2),
ldt_hf(Ns2,As,Hs).
dt_hf(Ns,[],Ns).
dt_hf(Ns,[a(X,Y)|As],[X>Y|Hs]) :-
delete(Ns,X,Ns1),
delete(Ns1,Y,Ns2),
dt_hf(Ns2,As,Hs).
human_to_gterm(HF,digraph(Ns,As)) :- memberchk(_>_,HF), !,
hf_dt(HF,Ns1,As1), sort(Ns1,Ns), sort(As1,As).
human_to_gterm(HF,graph(Ns,Es)) :-
hf_gt(HF,Ns1,Es1), sort(Ns1,Ns), sort(Es1,Es).
hf_gt([],[],[]).
hf_gt([X-Y/I|Hs],[X,Y|Ns],[e(U,V,I)|Es]) :- !,
sort0([X,Y],[U,V]), hf_gt(Hs,Ns,Es).
hf_gt([X-Y|Hs],[X,Y|Ns],[e(U,V)|Es]) :- !,
sort0([X,Y],[U,V]), hf_gt(Hs,Ns,Es).
hf_gt([H|Hs],[H|Ns],Es) :- hf_gt(Hs,Ns,Es).
hf_dt([],[],[]).
hf_dt([X>Y/I|Hs],[X,Y|Ns],[a(X,Y,I)|As]) :- !,
hf_dt(Hs,Ns,As).
hf_dt([X>Y|Hs],[X,Y|Ns],[a(X,Y)|As]) :- !,
hf_dt(Hs,Ns,As).
hf_dt([H|Hs],[H|Ns],As) :- hf_dt(Hs,Ns,As).
sort0([X,Y],[X,Y]) :- X @=< Y, !.
sort0([X,Y],[Y,X]) :- X @> Y.
path(G,A,B,P) :- path1(G,A,[B],P).
path1(_,A,[A|P1],[A|P1]).
path1(G,A,[Y|P1],P) :-
adjacent(X,Y,G), \+ memberchk(X,[Y|P1]), path1(G,A,[X,Y|P1],P).
adjacent(X,Y,graph(_,Es)) :- member(e(X,Y),Es).
adjacent(X,Y,graph(_,Es)) :- member(e(Y,X),Es).
adjacent(X,Y,graph(_,Es)) :- member(e(X,Y,_),Es).
adjacent(X,Y,graph(_,Es)) :- member(e(Y,X,_),Es).
adjacent(X,Y,digraph(_,As)) :- member(a(X,Y),As).
adjacent(X,Y,digraph(_,As)) :- member(a(X,Y,_),As).
%! \begin{hint}
depth_first_order(Graph,Start,Seq) :- sorry.
%! \end{hint}
%! \begin{solution}
depth_first_order(Graph,Start,Seq) :-
(Graph = graph(Ns,_), !; Graph = digraph(Ns,_)),
memberchk(Start,Ns),
clear_rdb(dfo),
recorda(dfo,Start,_),
(dfo(Graph,Start); true),
bagof(X,recorded(dfo,X,_),Seq).
dfo(Graph,X) :-
adjacent(X,Y,Graph),
\+ recorded(dfo,Y,_),
recordz(dfo,Y,_),
dfo(Graph,Y).
clear_rdb(Key) :-
recorded(Key,_,Ref), erase(Ref), fail.
clear_rdb(_).
%! \end{solution}?- depth_first_order(graph([a,b,c,d,e,f,g,h],[e(a,e),e(a,b),e(a,d),e(b,c),e(b,e),e(c,e),e(e,d),e(d,f),e(e,h),e(d,g),e(f,g),e(g,h)]),h,A).
:- module(_, _, [assertions, datafacts]).
:- push_prolog_flag(multi_arity_warnings, off).
:- use_module(library(idlists), [memberchk/2, subtract/3]).
:- use_module(library(sets),[ord_subset/2]).
:- use_module(library(sort)).
:- use_module(engine(hiord_rt),[call/2]).
:- use_module(library(aggregates), [findall/3]).
:- use_module(library(classic/classic_predicates), [delete/3]).
:- data edge/2.
:- data arc/2.
:- test connected_components(G,Gs) : (G = graph([],[])) => (Gs = []) + (not_fails, is_det).
:- test connected_components(G,Gs) : (G = graph([a,b,c,d,e,f,g,h],[e(a,e),e(a,b),e(a,d),e(b,c),e(b,e),e(c,e),e(e,d),e(d,f),e(e,h),e(d,g),e(f,g),e(g,h)])) => (Gs = [graph([a,b,c,d,e,f,g,h],[e(a,e),e(a,b),e(a,d),e(b,c),e(b,e),e(c,e),e(e,d),e(d,f),e(e,h),e(d,g),e(f,g),e(g,h)])]) + (not_fails, is_det).
:- test connected_components(G,Gs) : (G = graph([a,b,c,d,e,f,g,h],[e(a,e),e(a,b),e(a,d),e(b,c),e(b,e),e(c,e),e(e,d),e(d,f),e(g,h)])) => (Gs = [graph([a,b,c,d,e,f],[e(a,e),e(a,b),e(a,d),e(b,c),e(b,e),e(c,e),e(e,d),e(d,f)]),graph([g,h],[e(g,h)])]) + (not_fails, is_det).
sorry :- throw(not_solved_yet).
alist_gterm(Type,AL,GT):- nonvar(GT), !, gterm_to_alist(GT,Type,AL).
alist_gterm(Type,AL,GT):- atom(Type), nonvar(AL), alist_to_gterm(Type,AL,GT).
gterm_to_alist(graph(Ns,Es),graph,AL) :- memberchk(e(_,_,_),Es), ! ,
lgt_al(Ns,Es,AL).
gterm_to_alist(graph(Ns,Es),graph,AL) :- !,
gt_al(Ns,Es,AL).
gterm_to_alist(digraph(Ns,As),digraph,AL) :- memberchk(a(_,_,_),As), !,
ldt_al(Ns,As,AL).
gterm_to_alist(digraph(Ns,As),digraph,AL) :-
dt_al(Ns,As,AL).
lgt_al([],_,[]).
lgt_al([V|Vs],Es,[n(V,L)|Ns]) :-
findall(T,((member(e(X,V,I),Es) ; member(e(V,X,I),Es)),T = X/I),L),
lgt_al(Vs,Es,Ns).
gt_al([],_,[]).
gt_al([V|Vs],Es,[n(V,L)|Ns]) :-
findall(X,(member(e(X,V),Es) ; member(e(V,X),Es)),L), gt_al(Vs,Es,Ns).
ldt_al([],_,[]).
ldt_al([V|Vs],As,[n(V,L)|Ns]) :-
findall(T,(member(a(V,X,I),As), T=X/I),L), ldt_al(Vs,As,Ns).
dt_al([],_,[]).
dt_al([V|Vs],As,[n(V,L)|Ns]) :-
findall(X,member(a(V,X),As),L), dt_al(Vs,As,Ns).
alist_to_gterm(graph,AL,graph(Ns,Es)) :- !, al_gt(AL,Ns,EsU,[]), sort(EsU,Es).
alist_to_gterm(digraph,AL,digraph(Ns,As)) :- al_dt(AL,Ns,AsU,[]), sort(AsU,As).
al_gt([],[],Es,Es).
al_gt([n(V,Xs)|Ns],[V|Vs],Es,Acc) :-
add_edges(V,Xs,Acc1,Acc), al_gt(Ns,Vs,Es,Acc1).
add_edges(_,[],Es,Es).
add_edges(V,[X/_|Xs],Es,Acc) :- V @> X, !, add_edges(V,Xs,Es,Acc).
add_edges(V,[X|Xs],Es,Acc) :- V @> X, !, add_edges(V,Xs,Es,Acc).
add_edges(V,[X/I|Xs],Es,Acc) :- V @=< X, !, add_edges(V,Xs,Es,[e(V,X,I)|Acc]).
add_edges(V,[X|Xs],Es,Acc) :- V @=< X, add_edges(V,Xs,Es,[e(V,X)|Acc]).
al_dt([],[],As,As).
al_dt([n(V,Xs)|Ns],[V|Vs],As,Acc) :-
add_arcs(V,Xs,Acc1,Acc), al_dt(Ns,Vs,As,Acc1).
add_arcs(_,[],As,As).
add_arcs(V,[X/I|Xs],As,Acc) :- !, add_arcs(V,Xs,As,[a(V,X,I)|Acc]).
add_arcs(V,[X|Xs],As,Acc) :- add_arcs(V,Xs,As,[a(V,X)|Acc]).
ecl_to_gterm(GT) :-
findall(E,(edge(X,Y),E=X-Y),Es), human_gterm(Es,GT).
acl_to_gterm(GT) :-
findall(A,(arc(X,Y),A= >(X,Y)),As), human_gterm(As,GT).
human_gterm(HF,GT):- nonvar(GT), !, gterm_to_human(GT,HF).
human_gterm(HF,GT):- nonvar(HF), human_to_gterm(HF,GT).
gterm_to_human(graph(Ns,Es),HF) :- memberchk(e(_,_,_),Es), !,
lgt_hf(Ns,Es,HF).
gterm_to_human(graph(Ns,Es),HF) :- !,
gt_hf(Ns,Es,HF).
gterm_to_human(digraph(Ns,As),HF) :- memberchk(a(_,_,_),As), !,
ldt_hf(Ns,As,HF).
gterm_to_human(digraph(Ns,As),HF) :-
dt_hf(Ns,As,HF).
lgt_hf(Ns,[],Ns).
lgt_hf(Ns,[e(X,Y,I)|Es],[X-Y/I|Hs]) :-
delete(Ns,X,Ns1),
delete(Ns1,Y,Ns2),
lgt_hf(Ns2,Es,Hs).
gt_hf(Ns,[],Ns).
gt_hf(Ns,[e(X,Y)|Es],[X-Y|Hs]) :-
delete(Ns,X,Ns1),
delete(Ns1,Y,Ns2),
gt_hf(Ns2,Es,Hs).
ldt_hf(Ns,[],Ns).
ldt_hf(Ns,[a(X,Y,I)|As],[X>Y/I|Hs]) :-
delete(Ns,X,Ns1),
delete(Ns1,Y,Ns2),
ldt_hf(Ns2,As,Hs).
dt_hf(Ns,[],Ns).
dt_hf(Ns,[a(X,Y)|As],[X>Y|Hs]) :-
delete(Ns,X,Ns1),
delete(Ns1,Y,Ns2),
dt_hf(Ns2,As,Hs).
human_to_gterm(HF,digraph(Ns,As)) :- memberchk(_>_,HF), !,
hf_dt(HF,Ns1,As1), sort(Ns1,Ns), sort(As1,As).
human_to_gterm(HF,graph(Ns,Es)) :-
hf_gt(HF,Ns1,Es1), sort(Ns1,Ns), sort(Es1,Es).
hf_gt([],[],[]).
hf_gt([X-Y/I|Hs],[X,Y|Ns],[e(U,V,I)|Es]) :- !,
sort0([X,Y],[U,V]), hf_gt(Hs,Ns,Es).
hf_gt([X-Y|Hs],[X,Y|Ns],[e(U,V)|Es]) :- !,
sort0([X,Y],[U,V]), hf_gt(Hs,Ns,Es).
hf_gt([H|Hs],[H|Ns],Es) :- hf_gt(Hs,Ns,Es).
hf_dt([],[],[]).
hf_dt([X>Y/I|Hs],[X,Y|Ns],[a(X,Y,I)|As]) :- !,
hf_dt(Hs,Ns,As).
hf_dt([X>Y|Hs],[X,Y|Ns],[a(X,Y)|As]) :- !,
hf_dt(Hs,Ns,As).
hf_dt([H|Hs],[H|Ns],As) :- hf_dt(Hs,Ns,As).
sort0([X,Y],[X,Y]) :- X @=< Y, !.
sort0([X,Y],[Y,X]) :- X @> Y.
path(G,A,B,P) :- path1(G,A,[B],P).
path1(_,A,[A|P1],[A|P1]).
path1(G,A,[Y|P1],P) :-
adjacent(X,Y,G), \+ memberchk(X,[Y|P1]), path1(G,A,[X,Y|P1],P).
adjacent(X,Y,graph(_,Es)) :- member(e(X,Y),Es).
adjacent(X,Y,graph(_,Es)) :- member(e(Y,X),Es).
adjacent(X,Y,graph(_,Es)) :- member(e(X,Y,_),Es).
adjacent(X,Y,graph(_,Es)) :- member(e(Y,X,_),Es).
adjacent(X,Y,digraph(_,As)) :- member(a(X,Y),As).
adjacent(X,Y,digraph(_,As)) :- member(a(X,Y,_),As).
%! \begin{hint}
connected_components(G,Gs) :- sorry.
% Gs is the list of the connected components
% of the graph G (only for graphs, not for digraphs!)
% (gterm, list-of-gterms), (+,-)
%! \end{hint}
%! \begin{solution}
connected_components(graph([],[]),[]) :- !.
connected_components(graph(Ns,Es),[graph(Ns1,Es1)|Gs]) :-
Ns = [N|_],
component(graph(Ns,Es),N,graph(Ns1,Es1)),
subtract(Ns,Ns1,NsR),
subgraph(graph(Ns,Es),graph(NsR,EsR)),
connected_components(graph(NsR,EsR),Gs).
component(graph(Ns,Es),N,graph(Ns1,Es1)) :-
Pred =..[is_path,graph(Ns,Es),N],
include(Pred,Ns,Ns1),
subgraph(graph(Ns,Es),graph(Ns1,Es1)).
is_path(Graph,A,B) :- path(Graph,A,B,_).
% subgraph(G,G1) :- G1 is a subgraph of G
subgraph(graph(Ns,Es),graph(Ns1,Es1)) :-
ord_subset(Ns1,Ns),
Pred =.. [edge_is_compatible,Ns1],
include(Pred,Es,Es1).
include(_,[],[]).
include(P,[X|Xs],[X|S]) :-
call(P,X), !,
include(P,Xs,S).
include(P,[_|Xs],S) :-
include(P,Xs,S).
edge_is_compatible(Ns1,Z) :-
(Z = e(X,Y),!; Z = e(X,Y,_)),
memberchk(X,Ns1),
memberchk(Y,Ns1).
%! \end{solution}?- connected_components(graph([a,b,c,d,e,f,g,h],[e(a,e),e(a,b),e(a,d),e(b,c),e(b,e),e(c,e),e(e,d),e(d,f),e(g,h)]),A).
Miscellaneous Problems
Eight queens problem
:- module(_,_,[assertions]).
:- push_prolog_flag(multi_arity_warnings, off).
:- use_module(library(idlists), [memberchk/2]).
:- test queens_1(A,B) : (A = 4) => (B = [2,4,1,3]; B = [3,1,4,2]) + (not_fails, num_solutions(2)).
sorry :- throw(not_solved_yet).
%! \begin{hint}
queens_1(N,Qs) :- sorry.
% Qs is a solution of the N-queens problem
range(A,B,L) :- sorry.
% L is the list of numbers A..B
permu(Xs,Zs) :- sorry.
% the list Zs is a permutation of the list Xs
test(Qs) :- sorry.
% the list Qs represents a non-attacking queens solution
test(Qs,X,Cs,Ds) :- sorry.
% the queens in Qs, representing columns X to N,
% are not in conflict with the diagonals Cs and Ds
%! \end{hint}
%! \begin{solution}
% The first version is a simple generate-and-test solution.
queens_1(N,Qs) :- range(1,N,Rs), permu(Rs,Qs), test(Qs).
range(A,A,[A]).
range(A,B,[A|L]) :- A < B, A1 is A+1, range(A1,B,L).
permu([],[]).
permu(Qs,[Y|Ys]) :- del(Y,Qs,Rs), permu(Rs,Ys).
del(X,[X|Xs],Xs).
del(X,[Y|Ys],[Y|Zs]) :- del(X,Ys,Zs).
test(Qs) :- test(Qs,1,[],[]).
test([],_,_,_).
test([Y|Ys],X,Cs,Ds) :-
C is X-Y, \+ memberchk(C,Cs),
D is X+Y, \+ memberchk(D,Ds),
X1 is X + 1,
test(Ys,X1,[C|Cs],[D|Ds]).
%--------------------------------------------------------------
% Now, in version 2, the tester is pushed completely inside the
% generator permu.
queens_2(N,Qs) :- range(1,N,Rs), permu_test(Rs,Qs,1,[],[]).
permu_test([],[],_,_,_).
permu_test(Qs,[Y|Ys],X,Cs,Ds) :-
del(Y,Qs,Rs),
C is X-Y, \+ memberchk(C,Cs),
D is X+Y, \+ memberchk(D,Ds),
X1 is X+1,
permu_test(Rs,Ys,X1,[C|Cs],[D|Ds]).
%! \end{solution}?- queens_1(8,A).
Knight's tour
:- module(_,_,[assertions]).
:- push_prolog_flag(multi_arity_warnings, off).
:- use_module(library(idlists), [memberchk/2]).
:- test knights(A,B) : (A = 5) => (B = [1/5,3/4,5/5,4/3,5/1,3/2,1/3,2/5,4/4,5/2,3/1,1/2,2/4,4/5,5/3,4/1,2/2,1/4,3/3,2/1,4/2,5/4,3/5,2/3,1/1]) + (not_fails, num_solutions(2)).
sorry :- throw(not_solved_yet).
%! \begin{hint}
knights(N,Knights) :- sorry.
% Knights is a knight's tour on a NxN chessboard
closed_knights(N,Knights) :- sorry.
% Knights is a knight's tour on a NxN
% chessboard which ends at the same square where it began.
knights(N,M,Visited,Knights) :- sorry.
% the list of squares Visited must be
% extended by M further squares to give the solution Knights of the
% NxN chessboard knight's tour problem.
%! \end{hint}
%! \begin{solution}
knights(N,Knights) :- M is N*N-1, knights(N,M,[1/1],Knights).
closed_knights(N,Knights) :-
knights(N,Knights), Knights = [X/Y|_], jump(N,X/Y,1/1).
knights(_,0,Knights,Knights).
knights(N,M,Visited,Knights) :-
Visited = [X/Y|_],
jump(N,X/Y,U/V),
\+ memberchk(U/V,Visited),
M1 is M-1,
knights(N,M1,[U/V|Visited],Knights).
% jumps on an NxN chessboard from square A/B to C/D
jump(N,A/B,C/D) :-
jump_dist(X,Y),
C is A+X, C > 0, C =< N,
D is B+Y, D > 0, D =< N.
% jump distances
jump_dist(1,2).
jump_dist(2,1).
jump_dist(2,-1).
jump_dist(1,-2).
jump_dist(-1,-2).
jump_dist(-2,-1).
jump_dist(-2,1).
jump_dist(-1,2).
%! \end{solution}?- knights(5,A).
Arithmetic puzzle
:- module(_,_,[assertions]).
:- use_module(library(streams),[display/1,nl/0]).
:- use_module(library(classic/classic_predicates),[append/3]).
:- push_prolog_flag(multi_arity_warnings, off).
sorry :- throw(not_solved_yet).
%! \begin{hint}
equation(L,LT,RT) :- sorry.
% L is the list of numbers which are the leaves
% in the arithmetic terms LT and RT - from left to right. The
% arithmetic evaluation yields the same result for LT and RT.
%! \end{hint}
%! \begin{solution}
equation(L,LT,RT) :-
split(L,LL,RL), % decompose the list L
term(LL,LT), % construct the left term
term(RL,RT), % construct the right term
LT =:= RT. % evaluate and compare the terms
% term(L,T) :- L is the list of numbers which are the leaves in
% the arithmetic term T - from left to right.
term([X],X). % a number is a term in itself
% term([X],-X). % unary minus
term(L,T) :- % general case: binary term
split(L,LL,RL), % decompose the list L
term(LL,LT), % construct the left term
term(RL,RT), % construct the right term
binterm(LT,RT,T). % construct combined binary term
% binterm(LT,RT,T) :- T is a combined binary term constructed from
% left-hand term LT and right-hand term RT
binterm(LT,RT,LT+RT).
binterm(LT,RT,LT-RT).
binterm(LT,RT,LT*RT).
binterm(LT,RT,LT/RT) :- RT =\= 0. % avoid division by zero
% split(L,L1,L2) :- split the list L into non-empty parts L1 and L2
% such that their concatenation is L
split(L,L1,L2) :- append(L1,L2,L), L1 = [_|_], L2 = [_|_].
% do(L) :- find all solutions to the problem as given by the list of
% numbers L, and print them out, one solution per line.
do(L) :-
equation(L,LT,RT),
display(LT), display(' = '), display(RT), nl,
fail.
do(_).
%! \end{solution}?- do([2,3,5,7,11]).
K-regular simple graphs
English number words
:- module(_,_,[assertions]).
:- use_module(library(streams),[display/1, nl/0]).
sorry :- throw(not_solved_yet).
%! \begin{hint}
full_words(N) :- sorry.
% print the number N in full words (English)
% (non-negative integer) (+)
%! \end{hint}
%! \begin{solution}
full_words(0) :- !, display(zero), nl.
full_words(N) :- integer(N), N > 0, full_words1(N), nl.
full_words1(0) :- !.
full_words1(N) :- N > 0,
Q is N // 10, R is N mod 10,
full_words1(Q), numberword(R,RW), hyphen(Q), display(RW).
hyphen(0) :- !.
hyphen(Q) :- Q > 0, display('-').
numberword(0,zero).
numberword(1,one).
numberword(2,two).
numberword(3,three).
numberword(4,four).
numberword(5,five).
numberword(6,six).
numberword(7,seven).
numberword(8,eight).
numberword(9,nine).
%! \end{solution}?- full_words(N).
Nonograms
The puzzle goes like this: Essentially, each row and column of a rectangular bitmap is annotated with the respective lengths of its distinct strings of occupied cells. The person who solves the puzzle must complete the bitmap given only these lengths.
Problem statement: Solution: |_|_|_|_|_|_|_|_| 3 |_|X|X|X|_|_|_|_| 3 |_|_|_|_|_|_|_|_| 2 1 |X|X|_|X|_|_|_|_| 2 1 |_|_|_|_|_|_|_|_| 3 2 |_|X|X|X|_|_|X|X| 3 2 |_|_|_|_|_|_|_|_| 2 2 |_|_|X|X|_|_|X|X| 2 2 |_|_|_|_|_|_|_|_| 6 |_|_|X|X|X|X|X|X| 6 |_|_|_|_|_|_|_|_| 1 5 |X|_|X|X|X|X|X|_| 1 5 |_|_|_|_|_|_|_|_| 6 |X|X|X|X|X|X|_|_| 6 |_|_|_|_|_|_|_|_| 1 |_|_|_|_|X|_|_|_| 1 |_|_|_|_|_|_|_|_| 2 |_|_|_|X|X|_|_|_| 2 1 3 1 7 5 3 4 3 1 3 1 7 5 3 4 3 2 1 5 1 2 1 5 1For the example above, the problem can be stated as the two lists [[3],[2,1],[3,2],[2,2],[6],[1,5],[6],[1],[2]] and [[1,2],[3,1],[1,5],[7,1],[5],[3],[4],[3]] which give the "solid" lengths of the rows and columns, top-to-bottom and left-to-right, respectively. Published puzzles are larger than this example, e.g. 25 x 20, and apparently always have unique solutions.