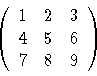Structure Inspection

Part of Prolog builtins are related to structure (functors) inspection: variables bound to structures can be accessed to find out the functor name, its arity, a given argument, etc. The two basic predicates for doing that are functor/3 and arg/3.

functor(F, N, A) succeeds when F is a complex structure whose arity is N and whose arity is A. It can be used to build new functors with fresh variables, or to obtain the name and arity of already built functors:

?- X = corn(loki, K, straight), functor(X, N, A).
   A = 3, N = corn, X = corn(loki,K,straight)

yes
?- functor(X, steam, 10).
   X = steam(_,_,_,_,_,_,_,_,_,_)

arg(F, N, Arg) succeeds when Arg is the N-th argument of functor F. Arguments start numbering at 1:

?- arg(1, corn(loki, K, straight), A).
   A = loki ?

yes
?- arg(2, corn(loki, K, straight), A).
   K = A ?

yes
?- arg(0, corn(loki, K, straight), A).

no
?- functor(X, steam, 10), arg(8, X, engine).
   X = steam(_,_,_,_,_,_,_,engine,_,_) ?

yes

Example 4.1   The above builtins can be used to test whether SubTerm can be unified with a subterm contained in Term:

subterm(Term, Term).
subterm(Sub,Term):-
    functor(Term,F,N),
    subterm(N,Sub,Term).

subterm(N,Sub,Term):-
    arg(N,Term,Arg),         % N > 0
    subterm(Sub,Arg).
subterm(N,Sub,Term):-
    N>1,
    N1 is N-1,
    subterm(N1,Sub,Term).

Term is traversed, element by element. If an argument of Term unifies with SubTerm, then SubTerm is already contained in Term (possibly after unifying one of its variables). Otherwise, the argument at hand is recursively traversed:

?- subterm(f(g), h(11, [oc, f(g)], loc)). 
yes 

?- subterm(f(T), h(11, [oc, f(g)], loc)). 
   T = g ? ; 
no 

?- subterm(f(T), h(11, [oc, f(g)], I)). 
   I = f(T) ? ; 
   T = g ? ; 
no

$\blacksquare$

Problem 4.1   The above example instantiates variables, either in the containing or in the contained term, in order to satisfy the requirement of being contained. Where exactly in the code is this performed? We will see later a way to work around this, if it is not desired. $\blacklozenge$

$\mathbf\therefore$

Another example of the application of structure-inspecting primitives is to use them to implement arrays. Arrays themselves are not available as a Prolog datatype, with associated operations, but they are easily simulated with structures. Any element of a structure can be accessed using its position. The name of the functor does not matter, actually. As an example, we will implement the predicate add_arrays/3 which will add the arrays passed in the first and second argument, and will leave the result in the third argument. The functor name we have chosen for the arrays is array/3:

add_arrays(A1,A2,A3):-
   functor(A1,array,N),           %% Equal length
   functor(A2,array,N),
   functor(A3,array,N),
   add_elements(N,A1,A2,A3).

add_elements(0,_A1,_A2,_A3).
add_elements(I,A1,A2,A3):-
   arg(I,A1,X1),                  %% I > 0
   arg(I,A2,X2),
   arg(I,A3,X3),
   X3 is X1 + X2,
   I1 is I - 1,
   add_elements(I1,A1,A2,A3).

The code first checks that the three arguments have the same functor name and arity; then the arrays are traversed from the end to the beginning (to use only one index, stopping at 0), and the corresponding elements in the arrays are added.

Note: some Prolog (and CLP) systems have a maximum fixed arity. Other implementation schemes (lists, for example, as done in the CLP arrays multiplication in Section 3.17.1) should be used for simulating larger arrays.

Problem 4.2   Write an add_matrices/3 predicate which can add matrices of arbitrary dimensions. Matrices will be represented using the functor mat/3, and are implemented by allowing the arguments of mat/3 to be themselves matrices, and not only numbers. For example, the structure

mat(mat(1, 2, 3), mat(4, 5, 6), mat(7, 8, 9))

would represent the matrix

$$\left( \begin{array}{ccc} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{array} \right)$$

I.e., its behavior should be as follows:

?- add_matrices(mat(mat(1, 2), mat(4, 3)), mat(mat(7, -2), mat(10, 4)), X).
   X = mat(mat(8, 0), mat(14, 7))

It should fail if the matrices to add do not have the same dimensions or the proper functor name. For simplicity, a number itself can be considered a matrix, so the query and answer

?- add_matrices(7, 4, X).
   X = 11

are both legal. $\blacklozenge$

$\mathbf\therefore$

There is also a utility predicate which converts (in a quite bizarre way) lists into structures and vice versa. The ``conversion'' is done as follows: the name of the structure is the first atom in the list, and the rest of elements of the list are the arguments of the structure. It is called univ, and its predicate name is =.., which is also defined as an infix operator:

?- date(9,february,1947) =.. L.
   L = [date,9,february,1947].

?- X =.. [+,a,b].
   X = a + b.

This builtin should be avoided unless really necessary: it is expensive in time and memory, and most time using it is a last resort for badly designed data structures and/or programs.